A Visual Introduction to Binary Search
A very basic and visual introduction to binary search.
A binary search is a search which can be performed on a sorted collection of elements and which works by continuously dividing up the search space in half by comparing the middle element to our search element and choosing which side to transverse. The same halving procedure is performed continuously until we either find the element that we’re looking for, or we end up with an empty interval and we know that our search element can’t be found.
Real World Analogy
Let’s say that we have a phone book, and that we need to search for a person’s number. Assuming that we have no index to reference, how do we perform our search?
Well, there’s the good old brute force way of doing it, which involves starting from the first name and checking if it matches with the name we’re looking for. If it does, we read the phone number and we’re done. Otherwise, we read the next word and repeat the same process continuously. If there are 100,000 names in the phone book, we’d have to go through 100,000 names, so this job will be very inefficient!
This is where a binary search would come in handy.
To perform a binary search, we take a look at the phone book, and we realize that the entries in it are sorted in ascending order. It begins with names starting from 'A' on the first page and the last page contains names starting with 'Z'. How can we use this to be more efficient? Well, we use this bit of information to continuously divide up our search space!
Let’s say that we’re looking for someone called ‘Bill’. First, we open the phone book so that we’re close to the middle page. We now look at the starting letters and the names which are present. We see that the entries all start with the letter 'M'! Now, we know that Bill starts with ‘B’, and since it precedes M, we know that we need to keep searching to the left of this page. We no longer need the second half of our phone book, which is to the right of current page, so we’ve effectively halving our search space!
Now, we limit your search to the left half. We find its middle page / element, and observe that the names on this page start with 'G'. Once again, we can see that Bill must be somewhere to the left of our element, so we once again restrict our search space and focus in on the left once again. We continually repeat this process until we find Bill, and we’re done.
Example
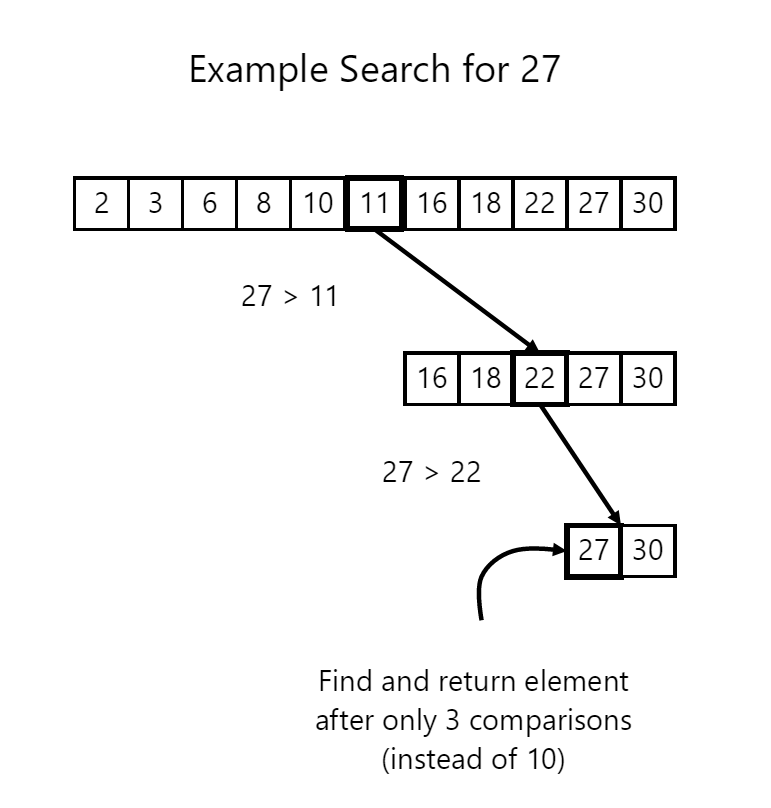
Let’s assume that we’re presented with the elements shown below:
Let’s assume that we were looking for 27 in the above array. Instead of having to look at each element – we simply take the middle element, compare it with our search value and keep going down until we find what we’re looking for:
We could therefore visualize a binary search as being a simple tree with each child node or nodes representing the halving our search space:
If we encounter a middle element less than our search value, we transverse the left tree; otherwise, we transverse the right and we repeat this step over and over again until there are no nodes to transverse!
Performance
How much more efficient is this than a regular linear search? Well, assuming that the phone book contains 100,000 names, we know that we have to search through just 17 entries (217 > 100,000) to find Bill. The larger the search space, the more benefits we see! Let’s assume that instead of 100,000, we have 1 million names. To perform a linear search, we’d need to go through all 1 million elements. Now, assuming that they’re sorted and we can use a binary search, we would just need to go through 20 elements to find whoever we’re looking for! Amazing, isn’t it?
In other words, since we keep halving our search space, it’ll take 2n steps (20 in the case of a million elements) to find our element instead of the normal n steps (1 million) we’d have to take using a linear search. Halving our search space each time means that our algorithm performance will equal to log n instead of n which makes quite a big difference when it comes to large arrays of elements!!
Implementation (in JavaScript):
function binarySearch(array, value) {
if (array.length === 0 || array[0] > value ||array[array.length - 1] < value) return undefined;
let left = 0;
let right = array.length - 1;
while(left <= right) {
const middleIndex = Math.floor(left + (right - left) / 2);
const middleValue = array[middleIndex];
if (value === middleValue) {
return middleIndex;
}
if (value < middleValue) {
right = middleIndex - 1;
} else {
left = middleIndex + 1;
}
}
return undefined;
}Finally
Binary search is a fundamental algorithm with wide-ranging applications across various domains in the software world. Its efficiency in searching and retrieving information from sorted data sets makes it a cornerstone in optimizing numerous operations. One key area where binary search shines is in searching and querying databases. In database management systems, binary search allows for quick data retrieval from large datasets, enabling efficient execution of queries and reducing response times.
In essence, binary search's ability to significantly reduce the search space in a systematic manner has led to its integration into countless real-world applications and software systems, fostering enhanced performance and responsiveness in a diverse range of computational tasks.