A Walk Through Combinatorics
An intuitive and visual focused walk-through and overview of combinatorics.
I recently got a chance to dive into the field of Combinatorics and decided to provide some of my own notes for anyone who’s interested in the topic and wants a high-level overview of this field. Many of the notes here are inspired by the book A Walk Through Combinatorics and a lot of the credit goes to Miklós Bóna. Noting this - let’s dive in!!
Introduction
Combinatorics is the branch of mathematics that studies how objects can be arranged, combined, or selected according to specific rules with a focus on patterns and relationships. By focusing on these relationships, we can gain a deeper understanding of how to model and count the objects in question. This intuition helps us solve many complex real-world problems including how to secure digital communications, understand genetic sequences, and efficiently plan trips. It’s influence extends to areas like artificial intelligence, cryptography, and game theory, making it indispensable for both theoretical research and real-world problem-solving.
The Pigeon Hole Principle
The Pigeonhole Principle is a simple yet powerful concept in combinatorics. It states that if you have more "pigeons" than "pigeonholes" and you want to put each pigeon into a pigeonhole, at least one pigeonhole must contain more than one pigeon.
In mathematical terms: If n items are put into m containers and n>m, then at least one container must hold more than one item.
Simple Example
Suppose you have a group of 13 people. Show that at least two of them were born in the same month.
Solution:
Identify the pigeons and pigeonholes: Here, the "pigeons" are the 13 people, and the "pigeonholes" are the 12 months of the year.
Apply the Pigeonhole Principle: Since there are more people (13) than months (12), by the Pigeonhole Principle, at least one month must have at least two people born in it. Thus, at least two people in this group were born in the same month.
Mathematical Induction (i.e. One Step at a Time)
Weak Induction
Weak induction, often simply called mathematical induction, is a proof technique used to show that a statement is true for all natural numbers. It works by proving two main steps:
Base Case: Prove that the statement is true for the first natural number (usually n=0 or n=1).
Inductive Step: Assume that the statement is true for some arbitrary natural number k (this assumption is called the inductive hypothesis). Then, use this assumption to prove that the statement is true for k+1.
Simple Example
Let's use weak induction to prove a simpler statement:
The sum of the first n odd numbers is n2
Proof:
First, we start off with our base case (n = 1):
The first odd number is 1. Since:
1 = 12
The base case holds.
Next, we go on to our inductive step. Assume that the statement is true for some arbitrary natural number k. That is, we can assume:
1 + 3 + 5 + … + (2k − 1) = k2
We need to prove that the statement is true for k+1. That is, we need to show:
1 + 3 + 5 + … + (2k − 1) + (2k + 1) = (k + 1)2
Using our original inductive hypothesis:
1 + 3 + 5 + … + (2k − 1) = k2
And subbing this into our new formula:
1 + 3 + 5 + … + (2k − 1) + (2k + 1) = (k + 1)2
1 + 3 + 5 + … + (2k − 1) = k2
We get:
k2 + (2k + 1) = (k + 1)2
And since we know that:
(k + 1)2 = k2 + 2k + 1
We know that our above statement holds and that:
k2 + (2k + 1) = (k + 1)2
= k2 + 2k + 1
Since the statement holds for k+1, by the principle of mathematical induction, the sum of the first n odd numbers is n2 for all natural numbers n.
Strong Induction
Strong induction, also known as complete induction, is similar to weak induction but with a slight difference in the inductive step. For weak induction, to prove that P(k+1) is true, you only assume that the previous step P(k) is true. For strong induction, you assume that all of the previous steps ( P(0), P(1), P(2), … , P(k) ) are true and use this to prove P(k + 1). In other words, weak induction is when you only use the immediately previous step. Strong induction is when you can use any previous step.
Simple Example
Let's use strong induction to prove a simpler statement:
Every natural number n ≥ 2 can be written as a product of one or more prime numbers.
Proof:
First, we start off with our base case (n = 2):
2 is a prime number, so it can be written as itself, which is a product of one prime number, thus the base case holds.
Next, we go on to our inductive step.
Assume that for all natural numbers m such that 2 ≤ m ≤ k, m can be written as a product of prime numbers. Now we need to prove that the statement is true for k+1:
If k + 1 is a prime number:
Then k + 1 itself is a product of one prime number (itself).
If k+1 is not a prime number:
Then k+1 can be written as a product of two natural numbers, say a and b, where 2 ≤ a ≤ k and 2 ≤ b ≤ k.
By the inductive hypothesis, both a and b can be written as products of prime numbers because they are both less than or equal to k.
Therefore, since k + 1 is a product of a and b:
k + 1 = a * b
We know that it can be written as a product of prime numbers which make up a and b:
k + 1 = (primes which produce a) * (primes which produce b)
Since the statement holds for the base case and the inductive step has been proven, by the principle of strong induction, every natural number n ≥ 2 can be written as a product of one or more prime numbers.
Elementary Counting Problems
Permutations
In simple terms, a permutation is a way of arranging items. The number of permutations of n distinct items is given by n! (n factorial), which is the product of all positive integers up to n. For 3 items, there are
3! = 3 × 2 × 1 = 6 permutations
Let’s consider a simple set of 3 items composed of A, B and C. If we want to list all the possible permutations (arrangements) of these three items, they would be:
ABC
ACB
BAC
BCA
CAB
CBA
Can you see why n different arrangements of n distinct items is n! (n factorial)?
We can get a good intuition for this by imagining that n people arrive at a doctor’s office at the same time. The doctor needs to treat them one by one, so they need to decide the order in which they’ll be served. Assuming there are n patients, there are n different choices which we can make on who to serve first. Knowing this then – how many choices do we have for which person goes second?
Well, we can observe that we already made a choice of who goes first, and we thus now have n – 1 patients to choose from for our 2nd choice. Once we make this choice, we have 1 less patient to once again choose from (thus obtaining n – 2) for our 3rd patient. Therefore, the number of orders in which the patients can be chosen in is:
n × (n - 1) × (n – 2) × ... × 2 × 1
= n! (n factorial)
Stirling’s Formula:
Stirling's formula is an approximation used to estimate the factorial of a large number n:
Stirling's formula becomes more accurate as n increases, making it a powerful tool for estimating factorials in mathematical analysis and in algorithms that deal with large numbers.
Permutations with Multisets
In our first example, we had a number of items (patients) and we assumed that no items could be repeated – but let’s now assume that we can have repetitions:
Example: Find the number of ways to arrange the letters in the word "AAB".
Solution: there are 3 distinct permutations of these letters provided below:
AAB
ABA
BAA
Notice that in this example, if all items were distinct, our formula would be 3! which equates to 6, but this time we only have 3. Why is this?
Well, and in multiset problems – we need to account for the fact that when items are repeated – some arrangements are identical because swapping identical elements results in an identical arrangement. If we were to look at our above example, we know that swapping two A’s in the AAB or ABA and BAA combinations doesn’t change the arrangement, so to adjust for the over-counting, we need to divide by the number of ways we can arrange the identical items within our set.
Thus, if you have n items in total, with n1 items of one type, n2 items of another type, and so on, the number of permutations is:
In the above formula, the numerator (n!) simply represents the total number of permutations were unique, and the denominator is our ‘adjustment factor’ created by the fact that we have identical elements where n1!⋅n2!⋯nk! adjusts for the fact that n1 items are identical, n2 items are identical, and so on, thereby correcting for over-counting.
In our earlier example (involving the unique permutations of ‘AAB’), we would obtain:
The above results in:
Another multiset example:
A box contains 3 red balls, 2 blue balls, and 1 green ball. How many distinct ways can you arrange these 6 balls in a row?
Solution:
First, we count the total number of elements we have:
Total balls = 3 red + 2 blue + 1 green = 6
Next, we identify the repetitions:
Number of red balls (n1) = 3
Number of blue balls (n2) = 2
Number of green balls (n3) = 1
Apply the multiset permutation formula:
We thus know that there are 60 distinct ways of arranging 3 red balls, 2 blue balls, and 1 green ball in a row.
Strings Over a Finite Alphabet
Next, we’ll examine problems where we aren’t merely arranging a given number of objects with specified usage limits. Instead, we’ll be creating strings or words using symbols from a finite set, called a finite alphabet. While we won’t need to specify how many times each symbol should appear, we might impose a restriction that each symbol can only appear once.
Example: Suppose you have an alphabet with 3 symbols: {A,B,C}. How many different 3-digit strings can you create using these symbols?
Solution: This time, we don’t have any limitations of which symbol we can pick in each position, so we can use each one of the 3 letters in our alphabet to get:
AAA
AAB
AAC
ABA
ABB
ABC
ACA
ACB
ACC
…
In the above examples, we enumerated over all of the possible combinations starting with the letter A – but we can keep going and substitute B and C as well. Enumerating over all arrangements thus nets us 3 * 9 = 27 different 3-letter strings.
We should be able to see the formula just by using our intuition:
Total number of possible combinations = (3 choices from A, B or C) × (3 choices from A, B or C) × (3 choices from A, B or C) = 3 × 3 × 3 = 27.
Our final solution is thus 33 = 27
Formula: The formula nk calculates the number of possible k-digit strings when using an n-element alphabet.
If you have n different symbols and want to create k-digit strings without repeating any symbols, the number of possible strings is given by the formula:
n × (n - 1) × (n – 2) × ... × (n – k + 1)
which can also be equivalently written down as:
Example:
If you have 5 symbols (A, B, C, D, E) and want to create 3-digit strings:
Choose and arrange 3 out of 5 symbols:
5 × 4 × 3 = 60
This is equivalent to using the formula:
In both cases, you get 60 possible 3-digit strings without repeating any symbols.
Bijections:
Imagine a large parking lot with many cars and many parking spaces. We don’t know the exact number of cars, but we know there are exactly 500 parking spaces. We suspect there are also 500 cars, but we’re not certain. How can we quickly test this idea? We can ask each car to park in a space. If every car finds a space and every space is filled, then we know there are exactly 500 cars. However, if some cars can’t find a space, it means there are more than 500 cars. Conversely, if some spaces remain empty, then there are fewer than 500 cars.
This technique of matching two sets element-wise and then conclude (in case of success) that the sets are equinumerous is very often used in combinatorial enumeration. Let us put it in a more formal context.
Let X and Y be two finite sets, and let f : X → Y be a function so that
If f(a) = f(b), then a = b, and
For all y ∈ Y there is an x ∈ X so that f(x) = y,
Then we say that f is a bijection from X onto Y. Equivalently, f is a bijection if for all y ∈ Y , there exists a unique x ∈ X so that f(x) = y.
In other words, a bijection matches the elements of X with the elements of Y , so that each element will have exactly one match.
The functions that have only one of the two defining properties of bijections also have their own names:
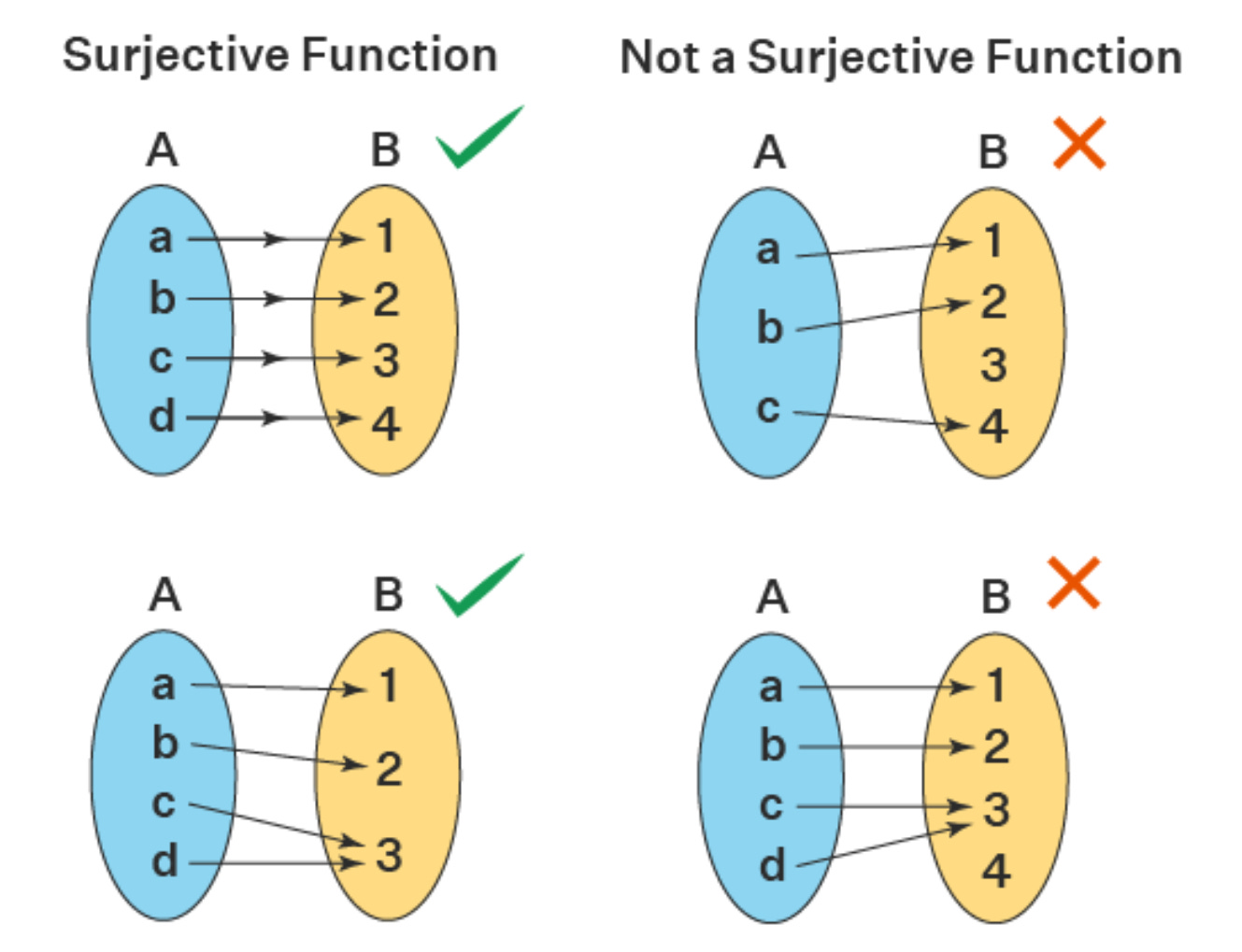
Injection:
If f satisfies criterion (1) (i.e. f(a) = f(b), then a = b) then we say that f is one-to-one or injective.
In the above image, we can observe that every element of set A is mapped to a unique element in set B. Further, if any element is set B is an image of more than one element of set A, then it is not a one-to-one or injective function.
Surjection:
If f satisfies criterion (2) (i.e. for all y ∈ Y there is an x ∈ X so that f(x) = y), then we say f is onto or surjective.
In other words, in a surjective function, every element of set B has been mapped from one or more than one element of set A. Also, the functions which are not surjective functions have elements in set B that have not been mapped from any element of set A.
Finally, two sets have the same size if and only if there is a bijection between them. Knowing this, we can use bijection to solve many combinatorial problems by converting one problem into another. Let’s show an example which illustrates this concept.
Simple Example:
How many ways are there to distribute 4 identical candies to 3 children?
Solution: To solve this problem, we'll use a bijection to relate it to a problem involving "stars and bars," a common combinatorial technique. Let’s first restate the problem in terms of stars and bars:
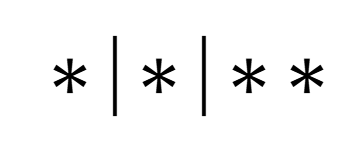
Think of the 4 candies as stars (∗) and the separations between different children as bars (∣). For example, distributing candies so that the first child gets 1 candy, the second child gets 2 candies, and the third child gets 1 candy can be represented as:
Some other examples are provided below:
1 candy for first child, 1 candy for second child, 2 candies for third child:
1 candy for first child, 3 candies for second child, 0 candies for third child:
0 candies for first child, 4 candies for second child, 0 candies for third child:
Seeing the bijection: we should be able to easily see that the problem of distributing 4 candies to 3 children is equivalent to finding the number of ways of arranging 4 stars and 2 bars in a sequence by looking at our examples, and we can thus proceed.
To solve the problem, we can treat it as a permutation problem involving multisets. We have count the ways of arranging 4 stars and 2 bars to get:
The total number of symbols (stars + bars) is 4 + 2 = 6, thus 6 is our numerator.
Since we have 4 identical stars and 2 bars, these are the values we have in the denominator to produce:
Using bijection, we transformed the problem of distributing candies into the problem of arranging stars and bars and so, we now know that there are 15 ways of distributing 4 identical candies to 3 children.
Choice Problems
In a local raffle, six numbers are chosen at random from a set of 50 numbers. To win the grand prize, you need to guess all six numbers correctly. How many different combinations are there to guarantee a win?
This type of problem is known as a "choice problem" in combinatorics. In these problems, we select certain subsets from a given set, often requiring the subsets to have a specific size. Unlike previous examples where the order mattered, here the order of the elements in the subset does not matter; for example, {5, 7, 9, 14} and {7, 5, 9, 14} are considered the same subset of the set of 50 numbers.
The number of ways to choose a subset of k elements from a set of n elements is crucial in combinatorics, so it has its own symbol and name which we denote as “n choose k” and which we represent below:
If you want to find out how many ways you can choose 6 numbers out of 50 distinct ones, we simple plug this into our formula to get:
Another Example:
A committee of 5 people is to be formed from a group of 10 candidates. How many different ways can the committee be formed?
Solution:
To solve this problem, we need to find the number of ways to choose 5 people out of 10.
Identify n and k:
n is the total number of candidates, which is 10.
k is the number of people to be chosen, which is 5.
Apply the Binomial Coefficient Formula:
The above gives us 252, so there are 252 different ways to form a committee of 5 people from a group of 10 candidates.
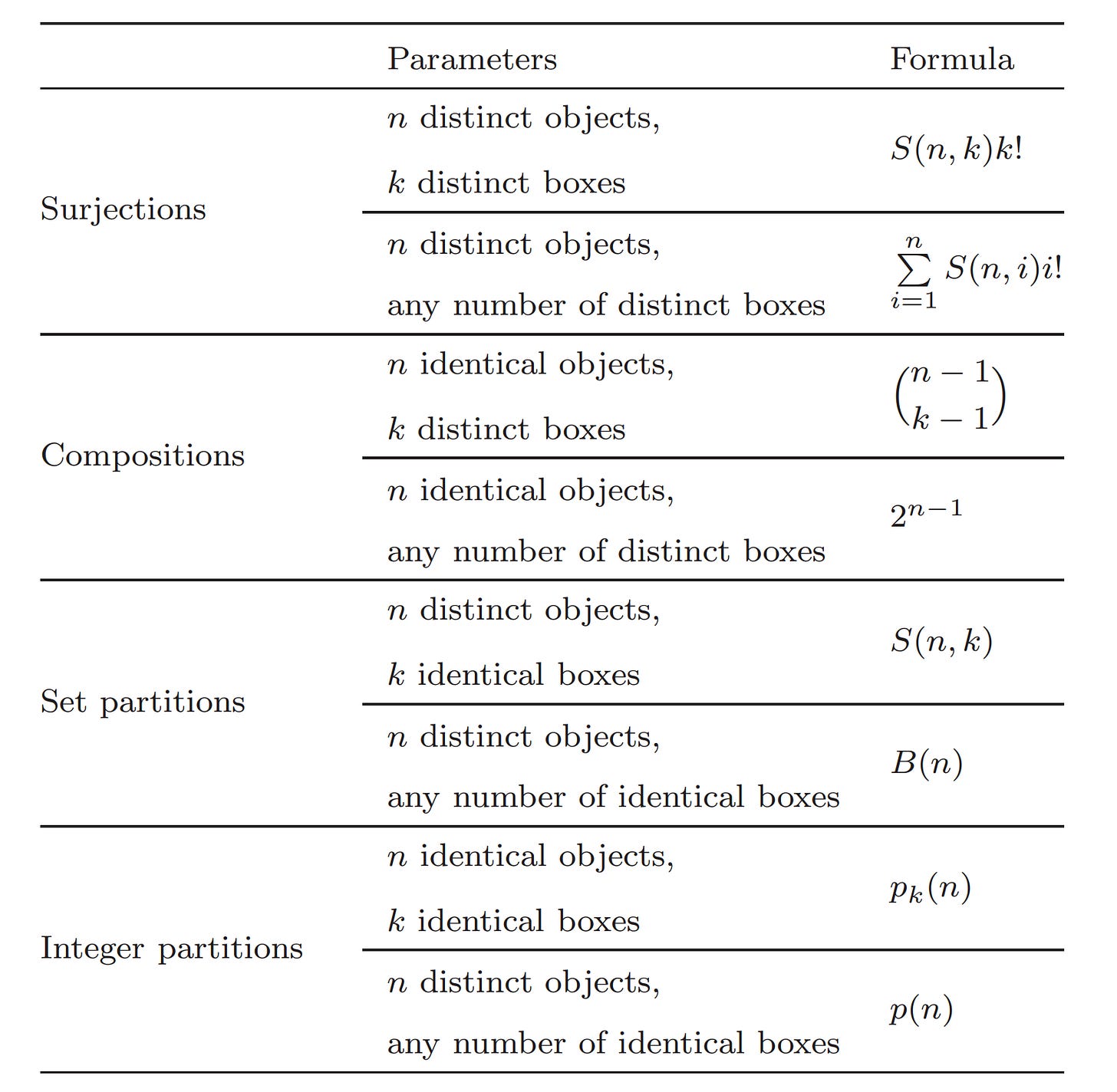
Enumeration / Counting Summary
The following table summarizes the enumeration theorems we went over in this section:
The Binomial theorem and Related Identities
The Binomial Theorem
The binomial theorem states that:
The theorem tells us how to expand (multiply out) a binomial that is raised to a power n. Let's look at a concrete example to make this clearer.
Example:
We can write out this expansion using our binomial theorem / formula:
Let’s calculate each term using the formula above:
When k = 0:
When k = 1:
When k = 2:
When k = 3:
When we combine all of our terms we finally get:
We should be able to see that the binomial theorem provides a way to expand expressions of the form (a+b)n into a sum of terms involving powers of a and b. The coefficients of these terms are given by the binomial coefficients, which can be calculated using factorials. This theorem is widely used in algebra and combinatorics.
Pascal’s Triangle
Pascal's triangle is a triangular array of numbers. Each number is the sum of the two numbers directly above it in the previous row. The first few rows of Pascal's triangle look like this:
Another fantastic illustration:
The numbers in Pascal's triangle are the binomial coefficients n choose k. Each row n of Pascal's triangle corresponds to the coefficients of the expanded form of (a + b)n.
As an example, the 4th row of Pascal's triangle is:
The binomial theorem states:
And when we expand it out we get:
And this relates directly to the row in our triangle:
The Binomial Theorem (General Version)
Let me be any real number. Then:
where the sum is taken over all non-negative integers n.
Divide and Conquer. Partitions.
In our previous coverage, we mainly focused on lists of objects, distinct or not, with repetitions allowed or not, and with the order of the elements on the list being relevant or not. Here, we will go one step further by discussing distribution problems.
Compositions
Suppose we have fifteen identical candies and we want to give them to three children: Emma, Jack, and Lily. Since the candies are identical, what matters is how many candies each child gets. To find out the number of ways we can distribute these candies, we need to know how many ways we can write 15 as a sum of three non-negative integers. The order in which the integers are written matters because it represents different distributions. For example, 3 + 7 + 5 is different from 7 + 3 + 5 because in the first case, Emma gets three candies, while in the second case, Emma gets seven.
Definition:
A sequence (a1, a2, … , ak) of integers where each ai ≥ 0 and a1 + a2 + ⋯ + ak = n is called a weak composition of n. If, in addition, each ai is positive for all i, then the sequence (a1, a2, … , ak) is called a composition of n.
Example:
If we have 15 candies and want to distribute them among Emma, Jack, and Lily, one possible weak composition of 15 could be:
Emma gets 2 candies,
Jack gets 4 candies,
Lily gets 9 candies.
This can be written as the sequence (2, 4, 9).
If the sequence were (4, 9, 2), it would mean Emma gets 4 candies, Jack gets 9 candies, and Lily gets 2 candies.
These different sequences represent different ways of distributing the candies, even though the sum is still 15.
Formula for Computing Weak Compositions
The number of weak compositions of a positive integer n into k parts is given by the binomial coefficient:
Example:
Let's solve the example of distributing 15 candies to three children (Emma, Jack, and Lily) using this formula.
Identify n and k:
n = 15 (the total number of candies)
k = 3 (the number of children)
Apply the Formula:
The number of weak compositions is given by:
Calculating the binomial coefficient 17 choose 2 gives us 136 and so there are 136 different ways to distribute 15 candies among 3 children.
For all positive integers n and k, the number of compositions of n into k parts is:
Example: Let's solve an example using this formula. Suppose we want to find the number of compositions of the number 8 into 3 parts.
Let’s first use our formula and plugin the correct components to find the correct solution:
Identify n and k:
n = 8 (the total number to be split)
k = 3 (the number of parts)
Apply the formula:
The above gives us an answer of 21, so there are 21 different compositions of 8 into 3 parts.
Explanation: A composition of n into k parts means breaking down n into k positive integers where the order of the integers matters. For example, the compositions of 8 into 3 parts could include sequences like (1, 2, 5) and (2, 1, 5), which are considered different because the order is different.
We can visualize this problem as a bijection into placing 2 dividers into 7 possible slots, so we need to choose 2 dividers out of our 7 available ones. As an example, the number 8 can be represented as:
And you should be able to visualize the possible slots we have to select from through the visual presented below:
To divide these 8 items into 3 parts, we must choose 2 of the available slots which we presented above. As an example, the partition (2, 4, 2) can be represented as:
As another example, the partition (2, 1, 5) could be represented as:
Since we need to select (choose) 2 slots out of 7 possible ones, we should be able to see the intuition behind our formula!!
For all positive integers n, the number of all compositions of n is:
Example and Explanation:
A composition of n is a way of writing n as a sum of positive integers where the order matters. For example, for n=4, the compositions include sequences like 1+1+1+1, 2+2, 1+3, and so on. When we compose n, we are effectively placing n−1 potential "dividers" between the numbers 1 through n−1 to create different parts.
As n example, to compose 4 into parts, we can visualize our possible dividers through the diagrams presented below:
For each position between the numbers, we have two choices: place a divider or not to place a divider. Since we have n−1 positions where we can either place or not place a divider, each position represents a binary choice. The total number of ways to make these choices is 2n−1 because there are n−1 positions and each position has 2 options. In the above example, we have 3 slots to choose from so our answer is:
Set Partitions
Let’s take the example of assigning balls to boxes. Partitions refer to instances where we assume that the balls are different, but the boxes are not.
A partition of the set [n] means dividing the set into non-empty groups so that each element is in exactly one group. The number of ways to partition [n] into k non-empty groups is represented by S(n, k). These numbers are called the Stirling numbers of the second kind.
Simplification:
A partition means dividing a set into groups where each group has at least one element and no element is left out. As an example, for set [3] = {1, 2, 3}, one partition into 2 groups could be {{1, 2}, {3}}.
We use [n] to denote the set of the first n positive integers. As an example [2] = {1, 2}.
When we use S(n, k) notation, we mean Stirling numbers of the second kind and it denotes the number of ways to partition the set [n] (first positive n integers) into k non-empty groups.
As an example, S(3, 2) is the number of ways to partition {1, 2, 3} into 2 groups. There are 3 such partitions and they are:
If we have to put n different balls into k different boxes then the number of ways to do this is k! · S(n, k). Indeed, first we can partition [n] into k non-distinguishable blocks in S(n, k) ways, then we can label the k blocks with labels 1, 2,...,k in k! different ways.
The number of all set partitions of [n] into nonempty parts is denoted by B(n), and is called the nth Bell number. We also set B(0) = 1.
Example:
B(3) is the number of ways to partition {1,2,3}. There are 5 such partitions:
There are 5 partitions, so B(3) = 5.
Integer Partitions
Now, let's assume that both the balls and the boxes are identical. This means the only thing that matters is the number of balls in each box. We want to find out how many ways we can write the number n as a sum of positive integers, where the order doesn't matter. For example, 4 = 3 + 1 is considered the same as 4 = 1 + 3.
More formally, let a1 + a2 + … + ak be the integers which equal to n. The sequence (a1, a2,...,ak) is called a partition of the integer n. The number of all partitions of n is denoted by p(n). The number of partitions of n into exactly k parts is denoted by pk(n).
We note that the word “partition” is used in a new meaning here.
Example:
The positive integer 5 has 7 partitions. Indeed, they are:
Therefore, p(5) = 7.
The problem of finding an exact formula for p(n) is even harder than that of finding an exact formula for S(n, k) (for which there is no formula). The approximate size of the number p(n) is provided by the following asymptotic formula:
Section Summary
A table summarizing our results is provided below:
Cycles in Permutations
Permutations can be viewed not only as linear orders of different objects, most often elements of [n], but also as functions from [n] to [n].
Example:
The permutation 312 can be viewed as the (bijective) function f: [3] → [3] defined by f(1) = 3, f(2) = 1, and f(3) = 2.
The advantage of this approach is that now one can define the product of two permutations on [n] by simply taking their composition as a composition of functions.
Another Example:
Let f = 312 and let g = 213. Then:
Therefore, fg = 321.
As these two examples show, multiplication of permutations is not a commutative operation, that is, it is not true in general that fg = gf.
Cycles in Permutations
Consider the permutation 321564. We can think of this permutation as a function g from the set [6] to itself. Let's examine g more closely: First, g(2) = 2. This means 2 stays in its place and is called a fixed point.
Second, g(1) = 3 and g(3) = 1. This means applying g twice returns 1 and 3 to their original positions. So, 1 and 3 swap places and form a 2-cycle.
Similarly, g(4) = 5, g(5) = 6, and g(6) = 4. Applying g twice gives g2(4) = 6, g2(5) = 4, and g2(6)=5. Applying g three times returns 4, 5, and 6 to their original positions. So, 4, 5, and 6 rotate among themselves and form a 3-cycle.
All permutations can be decomposed into the disjoint unions of their cycles.
Example:
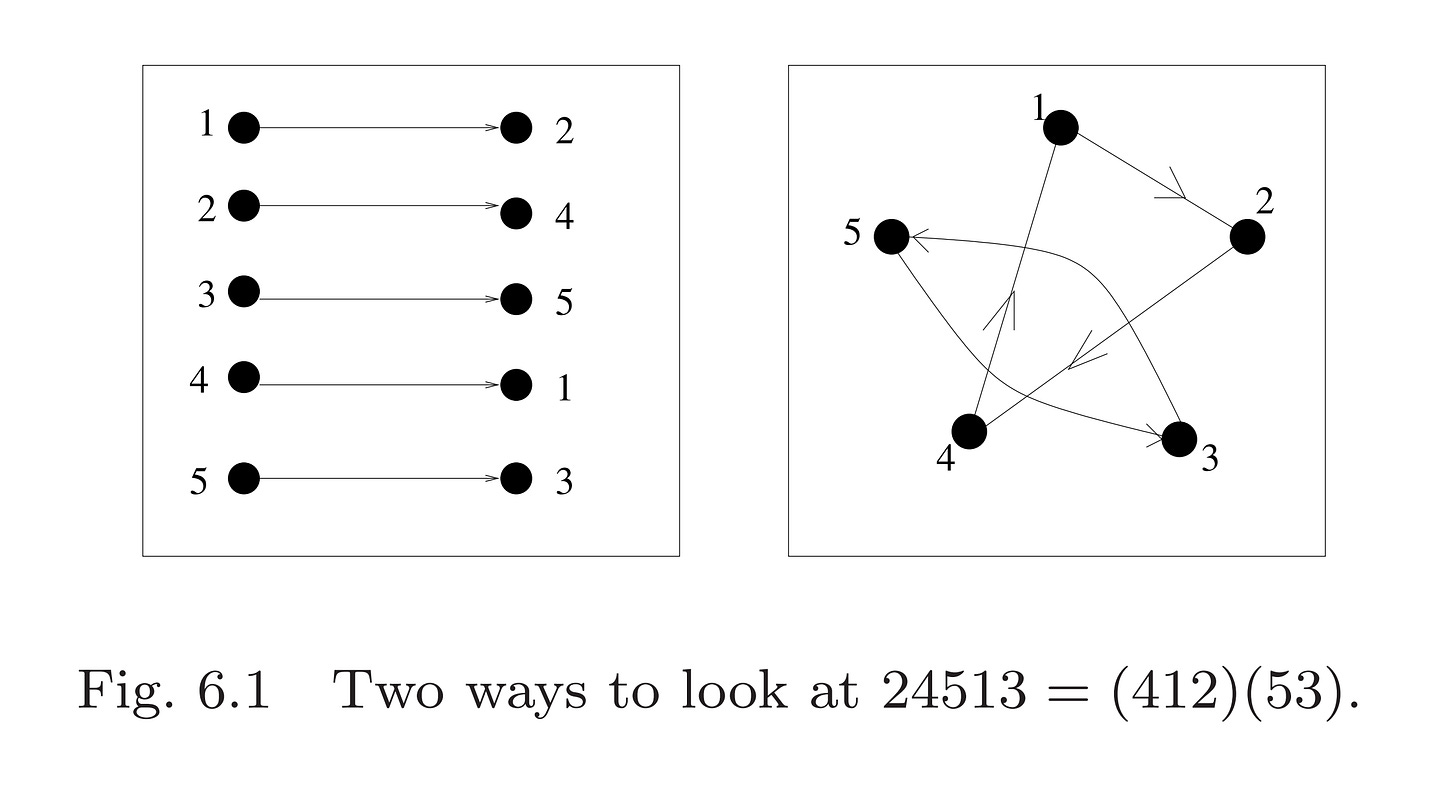
While the cycle decomposition of a permutation f is unique, the same cycle decomposition can be written in many different ways. The convention is to write entries that belong to the same cycle in parentheses. The order of the entries in the parentheses is such that j immediately follows i if f(i) = j. Furthermore, f(b) = a, where b is the last entry and a is the first entry in the parentheses. However, these principles do not preclude multiple notations for the same permutation. For instance, (241)(35) and (53)(412) denote the same permutation. In that permutation, f(2) = 4, f(4) = 1, f(1) = 2, f(3) = 5, and f(5) = 3.
We would like to avoid the danger of confusion caused by the phenomenon we have just described. Therefore, we will write our permutations in canonical cycle form. That is, each cycle will be written with its largest element first, and the cycles will be written in increasing order of their first elements. Thus the permutation f of our previous example has canonical cycle form (412)(53).
You Shall Not Over-count. The Sieve.
Enumerating the Elements of Intersecting Sets
There are 20 students in a high school who play the piano, and there are 15 students who play the guitar. Five students play both instruments. How many students play at least one of the two instruments?
Solution:
To find the number of students who play at least one of the two instruments, we use the principle of inclusion-exclusion:
Total = Piano + Guitar − Both (since we don’t want to double count)
= 20 + 15 – 5
= 30
So, 30 students play at least one of the two instruments.
Principle of Inclusion-Exclusion:
When counting the total number of students who play at least one instrument, we add the number of piano players and guitar players. Since the students who play both instruments are counted twice (once in the piano group and once in the guitar group), we subtract the number of students who play both to avoid double-counting.
Another Example:
In a high school, 25 students play the piano, 20 students play the guitar, and 15 students play the violin. Eight students play both the piano and the guitar, five students play both the piano and the violin, and six students play both the guitar and the violin. Two students play all three instruments. How many students play at least one of the three instruments?
Solution:
To find the number of students who play at least one of the three instruments, we use the principle of inclusion-exclusion for three sets:
Calculation:
Total = 25 + 20 + 15 – 8 – 5 – 6 + 2
Total = 43
So, 43 students play at least one of the three instruments.
General Formula for the Principle of Inclusion-Exclusion:
Let A1, A2,...,An be finite sets. Then:
Explanation:
The general formula for the Principle of Inclusion-Exclusion (PIE) involves adding the sizes of individual sets, subtracting the sizes of their pairwise intersections, adding the sizes of their triple intersections, and so on, alternately adding and subtracting higher-order intersections until the intersection of all sets is accounted for. This method ensures accurate counting by correcting for over-counting in a systematic way.
Let's illustrate this with an example using four sets A, B, C and D:
This ends part 1. I’ll be releasing Part 2 of this series which will attempt to cover the rest of the field. Once again, most of these sections and content are inspired by the book A Walk Through Combinatorics which I highly recommend - thank you for reading and if you enjoyed this content, please like and subscribe.





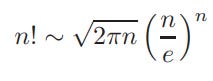



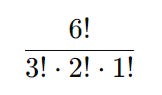

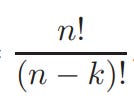







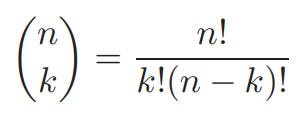

















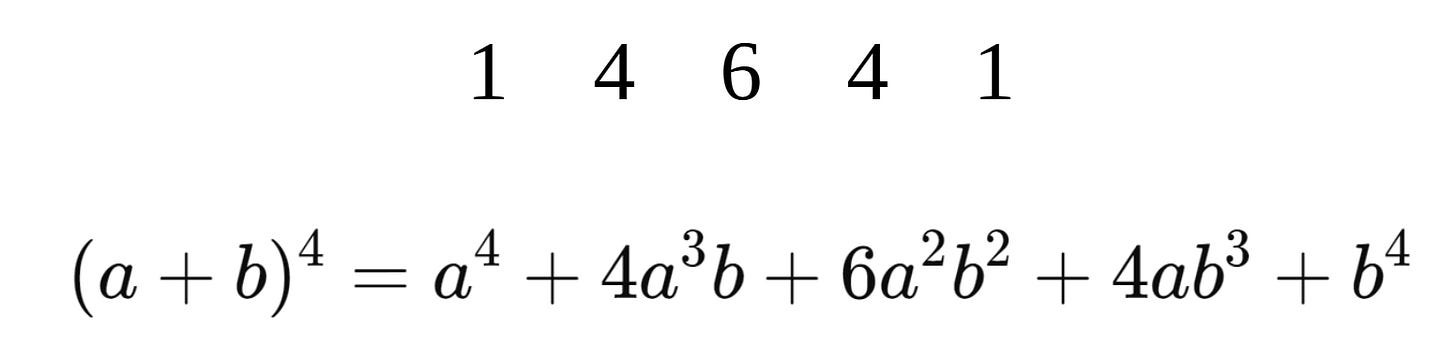
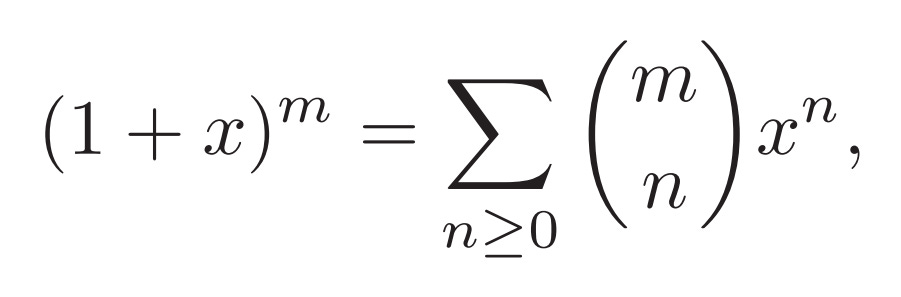










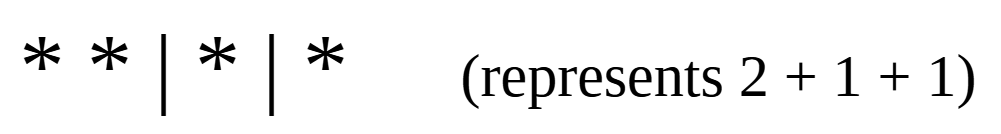

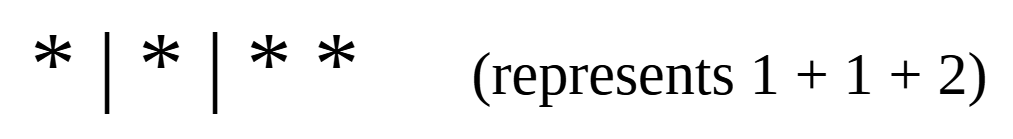














Just wanted to say thank you for writing this up. It's clear and intuitive, just perfect for a refresh