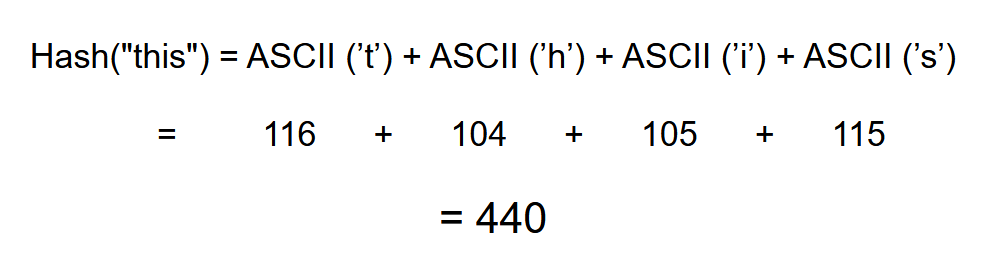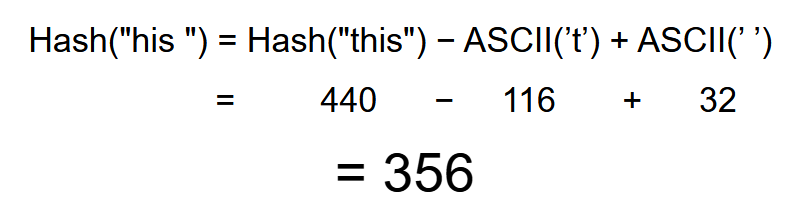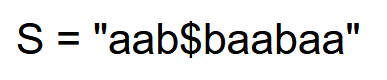A Walk-Through of String Search Algorithms
A walk-through of how some of the popular string-search algorithms work with a focus on the well-known Boyer-Moore and Robin-Karp algorithms.
We often don’t think about string-searching algorithms, but they play an incredibly important role in the real world. From searching keywords in a web browser to filtering spam emails, these algorithms power countless applications. Without efficient string-searching techniques, tasks we take for granted would be computationally expensive and time-consuming. Some of these algorithms form the backbone of modern computing, so we’ll dedicate this blog post to going through a few of them starting with my favorite: the Boyer-Moore algorithm.
Why do I love this algorithm so much? Well - this great explanation on why GNU grep is so fast pretty much sums it up:
Here's a quick summary of where GNU grep gets its speed. Hopefully you can carry these ideas over to BSD grep.
#1 trick: GNU grep is fast because it AVOIDS LOOKING AT EVERY INPUT BYTE.
#2 trick: GNU grep is fast because it EXECUTES VERY FEW INSTRUCTIONS FOR EACH BYTE that it *does* look at.
GNU grep uses the well-known Boyer-Moore algorithm, which looks first for the final letter of the target string, and uses a lookup table to tell it how far ahead it can skip in the input whenever it finds a non-matching character.
GNU grep also unrolls the inner loop of Boyer-Moore, and sets up the Boyer-Moore delta table entries in such a way that it doesn't need to do the loop exit test at every unrolled step. The result of this is that, in the limit, GNU grep averages fewer than 3 x86 instructions executed for each input byte it actually looks at (and it skips many bytes entirely).
The linked post is relatively short and does a great job in summarizing why grep is lightning fast, so I recommend you read all of the content, but in sum - the Boyer-Moore algorithm plays a vital role in making the sub-string or string-search process efficient. It does this by avoiding unnecessary work. How exactly this is done is explained below.
The Boyer-Moore Algorithm
Invented by Robert S. Boyer and J Strother Moore in 1977, this algorithm revolutionized string searching by introducing clever heuristics to drastically reduce the number of comparisons required. Unlike straightforward methods like the naïve approach (which checks every position in the text sequentially), the Boyer-Moore algorithm leverages mismatches to skip over large sections of the text.
The key insight behind the Boyer-Moore algorithm is founded on starting the pattern search at the last character rather than the first. Using this approach, it reduces the amount of work it has to do drastically. In addition to the tweak above, it also uses some key rules in how it processes the characters such that it can skip over large segments of text. Let’s go through a simple example in order to illustrate how it works.
Simple Example
Let's say our pattern p is the sequence of characters p1, p2, ..., pn and we are searching a string s:
In the above instance, our pattern is “AT THAT” and our search space is ‘WHICH FINALLY HALTS. AT THAT POINT…”
First, we set our index to point to the last element in our pattern string (shown below):
The Boyer-Moore algorithm uses the following rules to determine how far we can skip ahead:
Case 1:
If we try matching a character that is not in p, we can jump forward n characters where n = the length of our pattern string.
We can see that in our above instance, our index compares character ‘T’ in our pattern string to character ‘F’ in our search string. We know that the 'F' character is not present anywhere in our pattern p, so we know that we can advance n characters:
Case 2:
If we try matching a character whose last position is k from the end of p, we can then jump forward k characters.
In the above instance, our algorithm now compares the character ‘T’ in our pattern to the blank space in our search string. We know that the white space character’s last position in our pattern is exactly 4 characters from the end, and so we advance 4 characters:
Now, we once again scan backwards from i until we either succeed or we hit a mismatch. If the mismatch occurs k characters from the start of p and the mismatched character is not in p, then we can advance at least k characters.
In our above example, we first compare our first pattern character to our search string. Since they match and they both contain the character ‘T’, we move backwards to the next index and we now compare our pattern character ‘A’ to our search string character 'L'. Since the ‘L’ character is not present anywhere in our pattern p, we’re now allowed to move at least 6 characters! How did we get 6? Well, we know that our pattern length is 7 characters long, but we’ve already compared one character and so we take this into account:
However, we can actually do better than this!
Let’s go back to our original 2nd case which shows what we need to do when we encounter a character in our search string which is contained within our pattern p. We need to note that we actually have 2 main sub-cases to consider whenever dealing with this condition, and they’re illustrated below:
Sub-Case 1:
The matching suffix occurs somewhere else in the pattern:
In the above instance, we know that the matching sub-string is present somewhere else within our pattern p, so we shift ahead to align our pattern to the next match.
Sub-Case 2:
Only a part of the matching suffix occurs at the beginning of the pattern:
In the case above, we check whether any of the matched suffix matches the beginning of pattern, and if it does, we need to move ahead by n - (# of matching characters)!
Let’s go back to our original example. Once again, notice that in sub-case 2, we need to check whether a part of the matched string is present within the prefix of our pattern string p! Here, we check whether ‘T’ (our already matched character) is present at the beginning of our pattern. We see that it isn’t (our pattern starts with ‘A’, not ‘T’), so we know that we can actually jump forward by more than 6 characters! In this instance, we can actually advance ahead by 7, so that’s what we do instead:
At this point, we see that our index once again doesn’t have a match and that our pattern character ‘T’ is not equal to the blank character in our search string, so we can once again use the rules we encountered previously to determine how far ahead we can advance. Once again, we know that the blank character’s last position in our pattern is exactly 4 characters from the end, and so we advance 4 characters:
We then once again start comparing our characters one-by-one and moving backwards through our string. In the above case, we have a match for all seven characters, so we know that we’ve finally found a match!
Notice that the Bayer Moore algorithm saved us a ton of time by following the rules which we outlined! We only needed to perform 4 character comparison operations prior to arriving at the index which contained our matching string. A regular brute force search would have had to deal with 23 comparisons prior to finding the match!
Boyer-Moore isn’t the only well-known algorithm - there are a wide array of algorithms which attempt to minimize the amount of work which needs to be done (including the Knuth-Morris-Pratt (KMP) algorithm which we will cover later), but the reason I love Boyer-Moore is because it’s incredibly simple, efficient, and elegant!! Noting this, let’s move on to another interesting one: the Robin-Karp algorithm.
Robin-Karp Algorithm
Developed by Michael O. Rabin and Richard M. Karp in 1987, this algorithm introduces a clever twist: instead of directly comparing every character of the pattern with the text, it uses hashing.
Hashing allows us to turn the pattern and chunks of the text into compact numerical representations, making it much faster to check for matches. By comparing these hash values instead of individual characters, the algorithm streamlines the search process. It’s especially useful in cases where multiple patterns need to be matched or when working with very large datasets.
The elegance of Rabin-Karp lies in its simplicity and its adaptability to scenarios requiring fast pattern matching, like plagiarism detection, network packet filtering, and digital forensics. Here’s the step-by-step breakdown:
1. Hash the Pattern: First, compute a hash value for the pattern you’re searching for. A hash is a compact numerical representation of the pattern, designed so that different patterns typically result in different hash values.

Let’s go through a very simple example. Let’s say that we’re searching for the string ‘test’ within the text “this is a test text that contains test.” To generate hashes - we’re going to use a very simple algorithm: we’re simply going to add the sum of the ASCII values contained within the string. For ‘test’, our hash would thus result in:
Our hash is thus 448.
2. Hash Substrings of the Text: Slide a "window" of the same size as the pattern over the text and for each new position of the window, compute the hash of the substring within it.
Let’s go back to our prior example of searching for the string ‘test’ within the text “this is a test text that contains test.” We’ve already generated a hash value for our test string and we know that the integer it hashes to is 448. Now, we need to compute the hash for the first window within our search text. Since our search pattern has 4 characters, we know that our initial window is simply going to be the word “this” which hashes to:
The hash for “this” is thus 440.
3. Compare Hashes: As a next step, we simply compare the hash of the current substring to the hash of the pattern. If they match, we check the individual characters to confirm that the substring and the pattern are truly identical (since hash collisions can occur). Since we see that our hashes don’t match in the instance above (440 is not equal to 448), we slide our window by one position to the right and re-compute the new hash value.
We continue doing this until we find a match within our search string. Of course - re-computing each has for each string within our search string is incredibly inefficient, so we must find a way of computing these hash values without needing to do re-work.
4. Efficient Hash Updates: Instead of recalculating the hash from scratch for every new position, the algorithm uses a rolling hash—a method that efficiently updates the hash value when the window moves.
Let’s once again use our earlier example. Assuming that we already checked the first window (i.e. ‘this’ with hash 440) which resulted in a mismatch to our pattern match (i.e. ‘test with hash 448), we move on to generating a new hash for the next window. Notice though, that instead of re-computing a brand new hash from scratch — we can use the fact that our old window contains 3 of the same characters as our new one:
So - how can we use this information to save us time in generating a new hash? Well - to generate a new hash, we use the formula:
As an example, after computing the hash for ‘this’ - the next pattern will be ‘his ’ and thus the new hash will be:
We thus save a ton of work!
That pretty much covers how the Robin-Karp algorithm works. It’s not particularly fast when it comes to regular string searches, but one of the reasons why it’s well-known is due to the fact that it can be generalized for other applications, such as searching for multiple patterns at once or performing fingerprinting in areas like document similarity detection. By leveraging hash functions, the Robin-Karp algorithm excels in scenarios where preprocessing multiple patterns or comparing large sets of data is necessary, making it a versatile tool beyond simple string matching.
Some Other Interesting Algorithms
Knuth-Morris-Pratt (KMP)
Another key algorithm is the Knuth-Morris-Pratt (KMP). Like the Boyer-Moore algorithm, KMP uses the structure of the pattern to avoid unnecessary comparisons, but it works in a slightly different way.
The key idea behind KMP is to preprocess the pattern to gain insight into where the pattern can be safely shifted after a mismatch. It does this by creating a prefix table (also called a "partial match table"). For each position in the pattern, the prefix table records the length of the longest prefix that is also a suffix. As the algorithm searches for the pattern in the text, it compares the pattern’s characters with the characters of the text one by one. When a mismatch occurs, KMP looks at the prefix table to determine how far to shift the pattern.
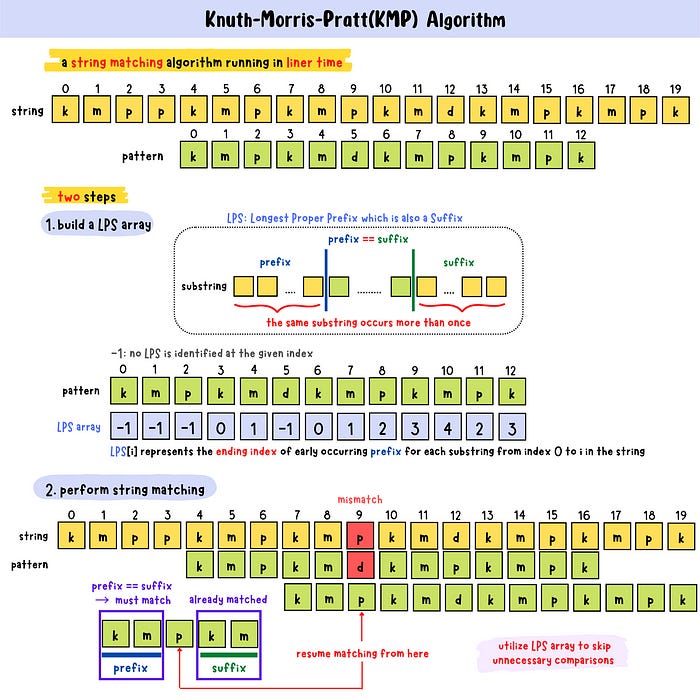
By shifting the pattern forward without re-examining previously matched characters, KMP ensures that every character of the text and pattern is checked only once, which leads to a linear time complexity.
Aho-Corasick
Aho-Corasick works by preprocessing all the patterns you want to search for into a special data structure called a trie (prefix tree). Then, it builds an automaton (a machine-like structure) from the trie, which allows it to quickly find all occurrences of any of the patterns in the text in one pass.
After the trie is built, the next step is to add failure links to it. These links are used to "fall back" to a previous state when a character mismatch occurs while searching the text.
For each character in the text:
If the character matches a transition in the trie, it follows the link.
If there is a mismatch, the failure link is used to skip to a previous state and resume the search from there.
At each step, the failure links guide us to the next possible matching state, so we never have to start over and all the matches are found efficiently. The trie and failure links allow the algorithm to quickly skip over unnecessary checks, making it much faster than checking each pattern one by one, especially when dealing with large texts and multiple patterns.
Z-Algorithm
The Z-algorithm is similar albeit a bit more efficient than the KMP algorithm. It finds matching substrings by building an array that tells it how much of the string matches its own prefix, starting from each position. This array is called the Z-array. For each position in the string, the value in the Z-array represents the length of the longest substring that starts at that position and matches the beginning of the string.
To build the Z-array, the algorithm uses two main ideas: it looks at the matches starting from the current position and uses information from previous matches to avoid redundant comparisons. A quick and straight-to-the-point overview of how to construct a z-array is provided below:
Let’s go through a simple example to show how the algorithm works:
Concatenate the pattern and text: As an example, let’s go through a pattern and text shown below:
We use the special character ‘$’ to separate our pattern from the text and the resultant string is:
This is the string we will compute our Z-array for.
Initialize the Z-array: Now we compute the Z-array for our concatenated string:
Our z-array is thus [10, 1, 0, 0, 0, 3, 1, 0, 2, 1].
Use the Z-array: The goal of the Z-algorithm is often to find where the pattern
Poccurs in the textT.To do this, we look at the Z-array values starting after the separator $ (which is at position 3). We know the length of the pattern P = "aab" is 3 — so we check for Z-values that are equal to or greater than 3, as they indicate a match of the pattern starting at those positions in the text. Since we see Z[5] = 3, we know that our pattern occurs within the substring.
That pretty much summarizes how it works.
The Z-algorithm is efficient because it computes the Z-array in linear time. It’s often used for efficiently searching for multiple patterns within the search text, as well as when solving problems like rotations and palindromic substrings. For simpler single-match tasks or short patterns, the Boyer-Moore algorithms still reigns supreme.
I’m going to end this post here, as it’s already incredibly long — but I highly recommend anyone who’s interested in this area to take a more in-depth look at each of the algorithms I overviewed above. If you liked enjoyed reading this post, please like and subscribe!