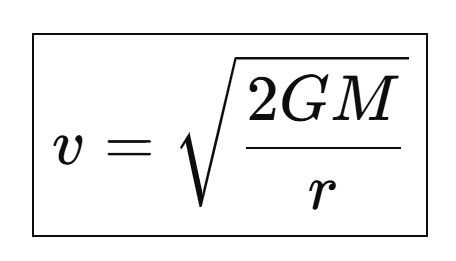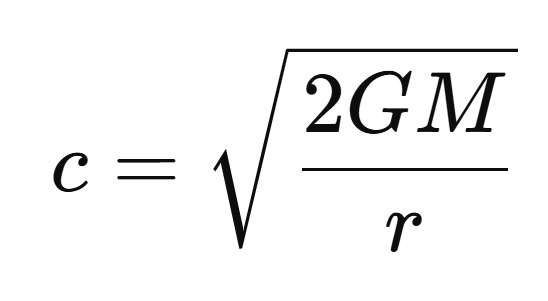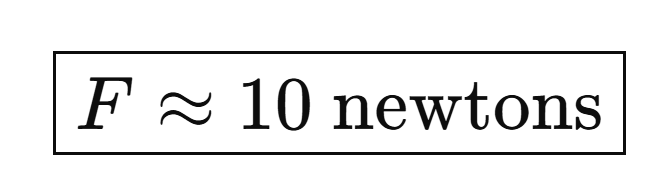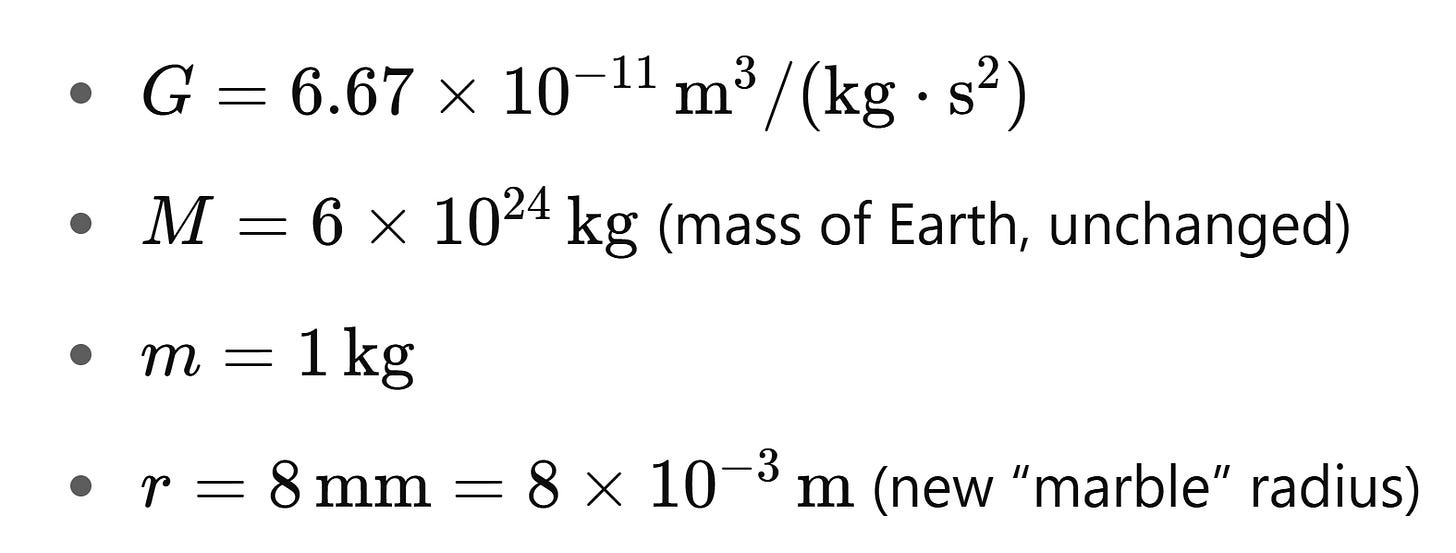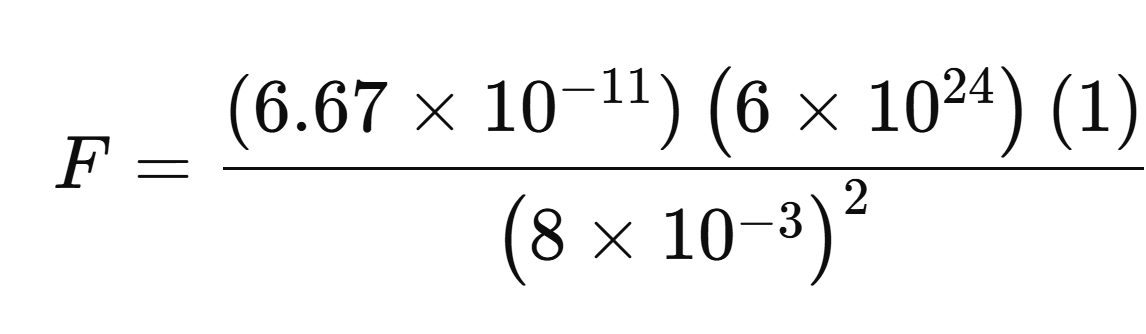An Intuitive Guide to Black Holes
An intuitive and visual-focused guide to what black-holes are (primarily lead by a simple thought-experiment).
Introduction
Black holes are a hugely interesting topic – but many of the explanations of what they actually are are mired in complexity, and I’m not a big fan of complexity and so I decided to do a more in-depth exploration of what they actually are and what they represent. This write-up will outline exactly what black holes are (as well as what their equations mean) in a more intuitive and visual manner. Saddle up – here we go.
What in the world is a black hole?
A black hole, in simple terms, is a region in space where the escape velocity (the speed needed to break free from its gravitational pull) exceeds the speed of light.
Imagine you're throwing a ball upward. If you throw it too softly, it falls back down.
Throw it harder, and it goes higher — but still comes back.
There's a specific speed that you’d need to throw it so it never comes back, and that’s called the escape velocity.
What exactly is earth’s escape velocity?
Let’s derive it. We need to use a few formulas to do this, and they’re provided below.
Gravitational Force Equation
The gravitational force F between two masses is:
In simple terms, the above equation tells us that the gravitational (attractive) force between the 2 masses is directly proportional to their masses (the higher their masses, the stronger the force) and inversely proportional to their distance squared (the further away they are, the weaker the force).
The above equation also abides by the inverse square law. The inverse square law not only applies to the force of gravity, but many different phenomena, including the electric field, light, sound or electromagnetic or nuclear radiation, which also obey this law. The law can easily be pictured through geometric intuition by visualizing an expanding sphere, with the force being distributed throughout the surface area of the sphere.
In other words, the force spreads out in an ever expanding spherical shell as the sphere itself moves radially and the surface area expands by r2 and so the field gets weaker as we expand outward.
Gravitational Potential Energy
This is the energy stored between Earth’s gravitational field and our ball. It can be represented by the equation shown below:
The negative sign shows that the ball is bound to the Earth and that gravity works to pull the objects closer. To escape, you’d need to add energy to free it. As you can probably observe, it’s extremely similar to our original gravitational force equation, and it simply outlines that the larger the distance between our 2 masses (r) – the less work we need to do in order to move our ball away from the gravitational pull that it receives from Earth. To use a more intuitive analogy, you can think of gravitational energy as “debt.” You owe the earth for being close to it and the further away you go, the smaller the debt becomes (less negative) until it finally disappears at infinity (where U would equal 0).
The negative sign means gravity traps the ball. To escape, you must repay this energy debt by giving the ball enough kinetic energy (KE) to balance the gravitational potential (U). Unlike the gravitational force (F ∝ 1 / r2), the potential energy (F ∝ 1 / r) weakens more slowly with distance. This is why escaping gravity requires a “lump sum” of energy upfront. In other words, to escape, you must balance this debt with kinetic energy, and that’s essentially what our escape velocity represents.
What is Energy? (The Universe’s Currency)
Energy is the "currency" of the universe — it’s what you "spend" to make anything happen. Think of it like money:
Do you need to move something? You spend energy (muscle power) in order to move it.
Do you need to keep a light bulb on? You need to spend energy (electricity – flowing electron energy) in order to keep the light on.
Do you need to launch a rocket? You need fuel in order to put it in motion.
Energy isn’t really anything physical – it measures your capability of doing something, and it comes in two primary forms: potential and kinetic energies.
Potential Energy: Stored "Savings"
You can think of the potential energy as the “stored” energy of our system. It represents something that’s waiting to be used and depends on the object’s position or state in whatever state-space it currently occupies. As an example, assuming that you put your baseball on a book-shelf – we can say that the object contains ‘potential’ energy by occupying a position on this shelf: if it falls, it can displace or move another object (i.e. do work) through the action of falling from this shelf – and the higher our shelf is, the more gravitational potential energy our ball has. In other words, you can think of potential energy as money in a bank account: you might not be able to directly see it, but it’s there and it’s ready to be spent.
Kinetic Energy: Energy in Motion
Kinetic energy is the energy of movement. It depends on an object’s current speed and mass. If you throw a baseball, it’s movement represents kinetic energy. The heavier the ball is or the faster you throw it – the more kinetic energy it has. You can imagine kinetic energy as being the cash you have in your wallet: it represents energy currently being used / put to work.
Total Energy
Now, energy is constantly being swapped between the 2 key forms we outlined above, and it cannot be created nor destroyed. In other words: we need to balance our account. To put this more formally, we say that total energy is always conserved. To escape Earth in other words, a rocket (or ball) must convert its kinetic energy into ‘climbing’ out of Earth’s gravitational ‘well’ (potential) energy to balance the books. To escape Earth’s gravity, an object needs enough kinetic energy (cash in hand) to pay off its gravitational potential energy (debt - i.e. money owed to Earth). Let’s balance the cosmic "checkbook" step by step.
The Energy Budget
As we should already know, at launch, our baseball has two types of energy:
Kinetic Energy (KE) (i.e. the energy from its current motion):
Gravitational Potential Energy (PE) (i.e. the ‘stored’ energy from being near the Earth):
Although we may have used the analogy of potential energy as being the “stored energy” in our system (thus being similar to money in a bank account) – in the above equation, we have a negative sign which we can now associate as being equal to owing your bank money (i.e. as being analogous to the debt you owe) and thus, positive energy terms equate to ‘stored’ money while negative terms equate to ‘owed’ money and we thus use the more appropriate debt term to represent this situation.
The total energy is equal to the kinetic energy plus the potential energy:
Total Energy = KE + PE
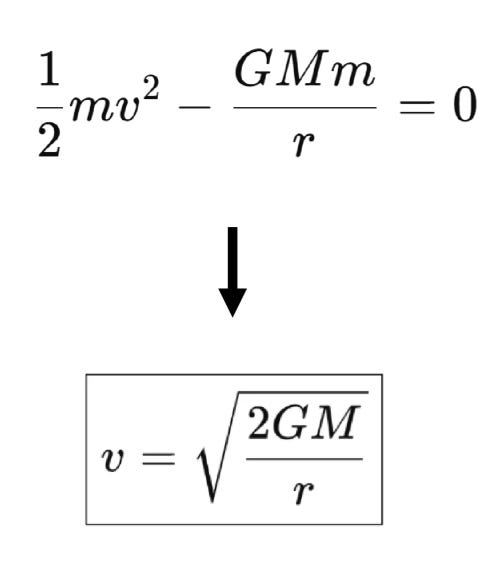
To escape Earth forever, the object must eliminate the potential energy within our books (i.e. no cash, no debt). So:
In order to find the escape velocity in other words, we need to solve for v. To do this, we first move the potential energy term to the other side:
Then, we cancel out the mass term from both sides:
To make the equation cleaner, we simply multiply both sides by 2:
Finally, we simply take the square root to obtain our formula for v (the escape velocity that we need in order to ‘balance or books’):
Let’s explain the above formula in a much more intuitive manner.
In order to escape’s Earth’s gravitational field, the distance between our ball and the Earth center of mass must be infinity:
In order to make the potential (U) equal to zero, r must be equal to infinity. Of course it will never reach infinity (because this is impossible) but conceptually if it were to stop before it gets to infinity, then there will be some potential energy because the potential energy never really goes away. But, hypothetically, when our distance is equal to infinity, the ball will eventually stop moving (so our kinetic energy at this point will be 0 (i.e. we will have 0 cash in our wallet)). When this happens, our potential energy will also be 0 as well (since we will no longer be effected by Earth’s gravitational energy) and so both of our energy terms would be 0 (0 debt and 0 cash). But energy can’t really be created nor destroyed. Essentially, this means that our total energy (kinetic + potential) must be equal to 0 all along this particular trajectory.
When you’re standing on the Earth’s surface, you’re deep in this "gravity well" so you have a big ‘debt’ (your potential energy is a large negative number) which you owe to Earth. If you want to leave Earth forever, you need enough cash (kinetic energy) to completely pay off that gravitational debt — and to totally escape it, your distance from Earth must be equal to infinity wherein both our potential and kinetic energy terms would be equal to 0. Since this is the case, what we’re doing with our equation above is simply ‘balancing’ our books and calculating how much kinetic energy (‘cash’) we would need in order to ‘pay off’ or balance the potential energy ‘debt’ such that the total within our system equals 0. To do this, we combine the equations (using the 2 terms we provided above), set them to equal 0 (KE + PE = 0) to ensure that our ‘books balance’ and we solve for v to obtain our escape velocity.
Deriving Earth’s Escape Velocity
Noting this, let’s continue on and plug in the right numbers to finally derive our finalized escape velocity.
Plugging in the appropriate values we obtain:
And so – Earth’s escape velocity is exactly 11,186 meters per second, and this equates to 11 kilometers per second (km/s). What we're saying here is that the escape velocity from the earth is 11 kilometers per second (which is approximately equal to 7 miles per second) and this is approximately equal to 25,000 miles per hour. That's quite a lot of up-front energy we have to put up in order to get our baseball out of Earth’s gravitational field!
This might seem like a lot, but it’s nothing compared to a black hole!!! You'll should be able to notice that 7 miles a second is a long way short of the speed of light which is 3 times 10 to the 8 meters a second.
Let’s remind ourselves of what a black hole once again represents:
“A black hole, in simple terms, is a region in space where the escape velocity exceeds the speed of light.”
So, we should be able to easily see that the earth is nowhere near to a black hole – a black hole needs an escape velocity of greater than the speed of light and earth’s escape velocity (of 11,000 meters per second) is nowhere near this!!
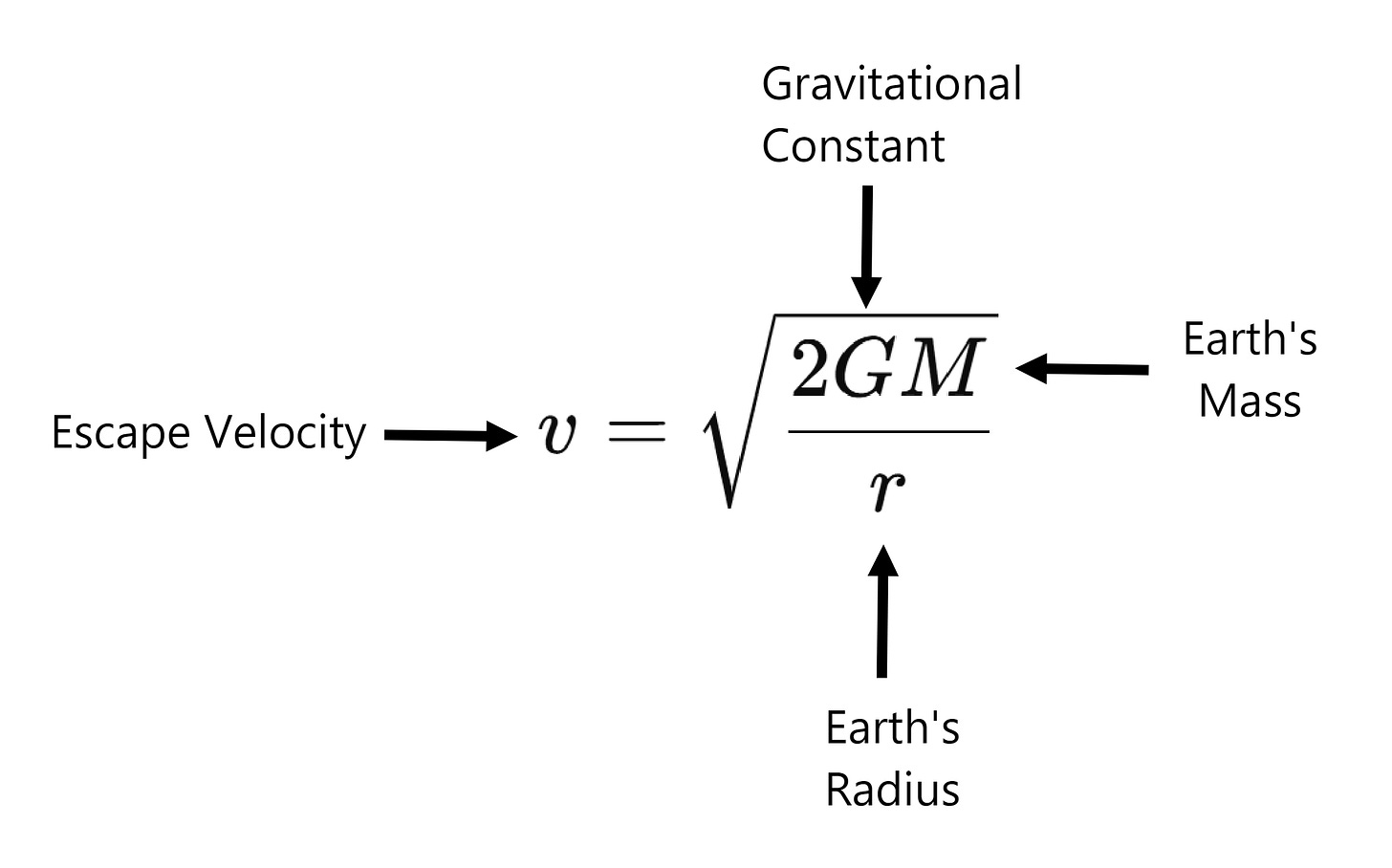
So let's just remind ourselves of what the original formula is for calculating the escape velocity:
You'll notice that v squared will get greater as r gets smaller. So – let’s do a little thought experiment. Let’s say that you take the earth and squash it (retaining all it’s current mass) so that it covers a much smaller area:
How much would we need to shrink it in order to make the v (the escape velocity) equal to the speed of light??
Well, we need to use mathematics to do this, and it’s actually quite simple. First, we take our original formula:
We want to know when the escape velocity v = c (the speed of light) and so we set v equal to c:
Now, to simplify things even further (so we can get the formula for r), we square both sides:
We re-arrange the above to solve for r and we get:
This is known as the Schwarzschild radius!!
This is the radius at which an object becomes a black hole. Let’s not stop here though – let’s plug in the appropriate values to find our radius and so now we have:
Plugging the values in we get:
After simplifying we finally get:
So -- if you compress the Earth into a sphere that has a radius of about 8.5 millimeters (a diameter of about 1.7 centimeters) it would become a black hole!!
In other words, if we could shrink all of Earth’s mass (about 6 times 1024 kilograms) into a sphere the size of a marble (~1.7 cms), the escape velocity would exceed the speed of light and at that point, and Earth would become a black hole from which not even light could escape!!
You may not be able to comprehend the gravitational force which Earth would have should someone, somehow, find a way to do this, so let’s do another thought experiment. Let’s inflate Earth once again to its regular size and see what impact placing a 1 kg weight on it has.
To do this, we’ll once again need our gravitational force formula and we’ll need to plug in the appropriate constants / inputs to obtain:
So we plug in the appropriate values to get:
We simplify even further to obtain:
We obtain 9.8 Newtons which we’ll round up to 10 to simplify things:
To be more precise, a 1 kg mass at Earth’s surface feels a gravitational force of about 10 Newtons (N). This may seem like a rather silly question, but now we ask: why doesn’t our 1 kg weight fall through our floor?
We know that gravity is “pulling down” on the 1 kg weight with about a 10 Newton force. If gravity were the only force acting on our weight, it would indeed accelerate downward!! In reality, the earth’s surface needs to “push back” upward with an equal and opposite force of about 10 Newtons in order to keep our weight in its stable position – but where does this force come from?
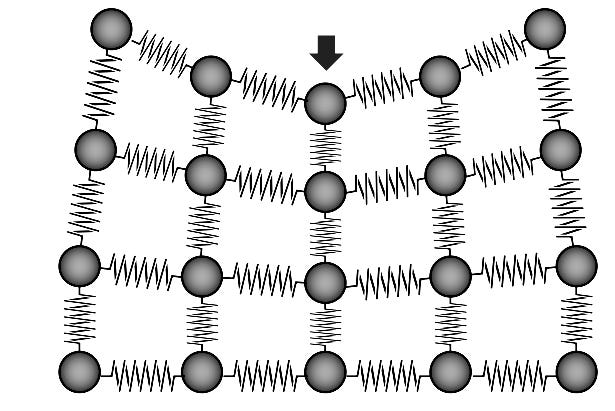
Well, we should all know by now that the floor in your house (or living area) is made out of concrete / wood, and these materials are made of atoms and molecules bound together. Those atoms form a rigid lattice held by electromagnetic (chemical) bonds. The best visual for this is to imagine these atoms and molecules being bound by springs that hold them together (and in equilibrium):
Now, you can imagine these springs as representations of the bonds which hold you floor (or any solid) together – and this is really why a solid is...well solid – there are ‘spring like’ bonds between these atoms which hold it together.
Now – you can imagine our 1 kg weight sitting on the floor: the weight’s force downward isn’t carried by one tiny point; it’s spread across the floor it is sitting on. Because the load is shared, no single spot gets overloaded and the floor doesn’t collapse.
In the same way, when you press on a solid material, that force is passed along through its network of atomic or molecular bonds – each bond takes just a tiny piece of the total load, so the material as a whole holds up rather than breaking.
You can think of it as being a trampoline woven by trillions of microscopic strings (atomic bonds). When you place a load (like a 10 Newton force) on these springs, it spreads out among them and each spring barely stretches. This means that those forces are stronger than the 10 Newton force (applied by gravity) to the 1 kilogram weight and so the 1 kilogram weight doesn't fall through the floorboards due to the molecular structure of the floorboards withstanding it.
But…what if gravity turned into a cosmic wrecking ball?
Now, let’s go back to squishing earth down to the size of an ordinary marble.
The question which I want to ask: what is the force acting on that 1 kilogram weight resting on its surface?
In this instance, we once again go back to our original formula and plug in the appropriate values:
Plugging in our values we get:
And finally, the final force in Newton’s is:
The answer: the force on our 1 kilogram weight is now an astounding 1019 Newtons. Suddenly, gravity isn’t a gentle tug—it’s a crushing avalanche.
In long form, this equates to:
10,000,000,000,000,000,000 Newtons
No known force (atomic or molecular) can resist this type of force!! Picture those trusty atomic springs again: on normal Earth, they share the load and they are thus able to over-come the gravitational potential energy from almost every object placed on them. Now – on marble-sized Earth, gravity’s force is a billion (1,000,000,000) times a billion times heavier: it’s like stacking every mountain on Earth onto a single spring. No atomic bond can withstand this!! The springs are ‘vaporized’ thus making gravity the winner!
In other words, the gravitational pull from Earth’s ‘surface’ drags everything inward. If you could squash the earth down to the size of a marble – the gravitational force would be so huge that nothing could stop it (due to Earth’s atomic bonds not being strong enough to hold it together) and it would thus carry on contracting under its own gravitational force and shrink until it essentially became a dimensionless point!!
This point is what we call a singularity. The point of no-return around the black hole from which nothing can escape is called the event horizon.
At that stage, all of Earth’s mass resides in a point with zero volume. If it had any width (or volume), the tremendous gravitational energy would just pull it in.
There is a radius around that singularity of 8 millimeters which says that anything inside that radius has an escape velocity of greater than the speed of light. The boundary is what we call the event horizon because gravity inside remains unstoppable and all matter inevitably falls into the singularity.
This is in essence of what a black hole represents: a celestial object so dense that no nearby matter or radiation can escape its gravitational field.
Often, this is described as the boundary within which the black hole's escape velocity is greater than the speed of light. However, a more detailed description is that within this horizon, all light-like paths (paths that light could take) and hence all paths in the forward light cones of particles within the horizon are warped so as to fall farther into the hole. Once a particle is inside the horizon, moving into the hole is inevitable.
How to Create a Black Hole
Now, you have to ask yourself: this is all great and it sounds interesting, but how in the world can a black-hole be created? Squashing the earth to the size of a marble doesn’t seem like a very feasible plan, after all – so how does the universe do it?
In nature, black holes aren’t made by squeezing planets—they’re born from the corpses of massive stars. And when I say massive, I mean stars at least 20 times heavier than our Sun. What keeps a star from collapsing in the first place is a process called nuclear fusion.
For most of its life, a massive star is caught in a tug‑of‑war between two forces. Gravity constantly tries to pull all its mass inward, while the heat and light generated by nuclear fusion push outward. You can think of fusion as the star’s “engine,” taking hydrogen nuclei and slamming them together into helium, releasing energy in the process.

Whenever two lighter nuclei fuse into one heavier nucleus, the process sheds a bit of mass as energy (E = mc²). That energy emerges as heat and light, creating an outward pressure that exactly counters gravity—so long as there’s hydrogen fuel in the core, the star stays intact and continues shining.
After millions of years, the hydrogen in the core starts to run out. The core contracts under gravity, heats up, and begins fusing helium into carbon, oxygen, and so on—building successively heavier elements all the way up to iron. Every new fusion stage lasts a shorter time than the last, but fusion of iron is special: it consumes energy instead of releasing it. Once a critical mass of iron builds up, there’s no more outward pressure from fusion. In an instant, gravity gains the upper hand.
Now, remember those atomic "springs" that held up our 1 kg weight? Here, they don’t just fail—they’re annihilated. Gravity ramps up to unimaginable forces (around 1030 Newtons per square meter) and the imploding core reaches densities so extreme that protons and electrons merge into neutrons. If the remaining core mass is around 1.4–3 solar masses, neutron degeneracy pressure stops the collapse, leaving behind a neutron star. But if the dead star’s core is more massive—say, five or ten times our Sun’s mass—the neutron star gambit fails. Even neutron degeneracy pressure (the quantum mechanical force that keeps neutrons from being squeezed into the same space) can’t halt the collapse. In a dramatic final act, nothing remains to hold the core up, and it shrinks below its own Schwarzschild radius (the point of no return) becoming a black hole. The star’s outer layers rebound off the collapsing core and explode outward in a brilliant supernova, briefly outshining an entire galaxy, while the core vanishes into a singularity.
In other words, creating a black hole is less like squeezing the Earth into a marble and more like building up a massive star, letting it burn brightly for millions of years, then watching as it exhausts its nuclear fuel and succumbs to gravity’s ruthless pull. From the fiery forge of fusion to the final, crushing collapse, black holes are born in one of nature’s most spectacular fireworks shows—and therein lies gravity’s ultimate triumph.
Final Note
A big thank you to all my supporters and to my paid subscribers – this is an ad free publication and I appreciate the support!!
Credits / References
Stock photos:
Earth image: https://pixabay.com/illustrations/earth-world-planet-globe-1303628/
1 kg weight image: https://openclipart.org/detail/190320/1kg-weight
Event horizon (Wikipedia entry): https://en.wikipedia.org/wiki/Event_horizon
Fusion image source: https://commons.wikimedia.org/wiki/File:FusionintheSun.svg