Grokking Hash Array Mapped Tries (HAMTs)
A simple and intuitive explanation of what Hash Array Mapped Tries are and where they're used.
Prerequisite Reading
Prior to understanding HAMTs, you’ll need to understand how hash tables and tries work. I already made a basic intro to hash tables which you can access here:
A great introduction and overview of what tries are is provided below:
HAMTs (Hash Array Mapped Tries)
A Hash Array Mapped Trie (HAMT) is a data structure that combines the benefits of hash tables and tries to efficiently store and retrieve key-value pairs. It is commonly used in computer science to implement associative arrays or dictionaries.
In a HAMT, keys are hashed to determine their storage location within an array, called a hash array. Each entry in the hash array can store multiple key-value pairs, allowing efficient memory utilization. If multiple keys hash to the same array index, a trie-like structure is used to resolve collisions.
Example illustrating how an HAMT works:
Suppose we have a HAMT that stores words and their corresponding definitions. For simplicity, we’ll use a simple hash table that only has four slots for storing values and which we index using two bits.
Let's say we want to store the following key-value pairs:
"apple" -> "a fruit"
"banana" -> "a tropical fruit"
"cat" -> "a small animal"
Initially, the HAMT is empty.
We start by inserting the first key-value pair, "apple" -> "a fruit". The key "apple" is hashed, and the resulting index in the hash array is determined. Let’s assume that the hash for “apple” is composed of 32 bits, but we use the first 2 bits in order to find the correct index in our table. In this instance, let’s assume that the first 2 bits of our hash are 01. Since the array at the calculated index is empty, we store the key-value pair directly in that position.
Next, we insert "banana" -> "a tropical fruit".
Again, the key is hashed, and the corresponding index is found in the hash array. Let’s assume that the computed hash value for our key starts with 10. We can see that this index in our array is once again empty, so we once again store our value directly within the hash table:
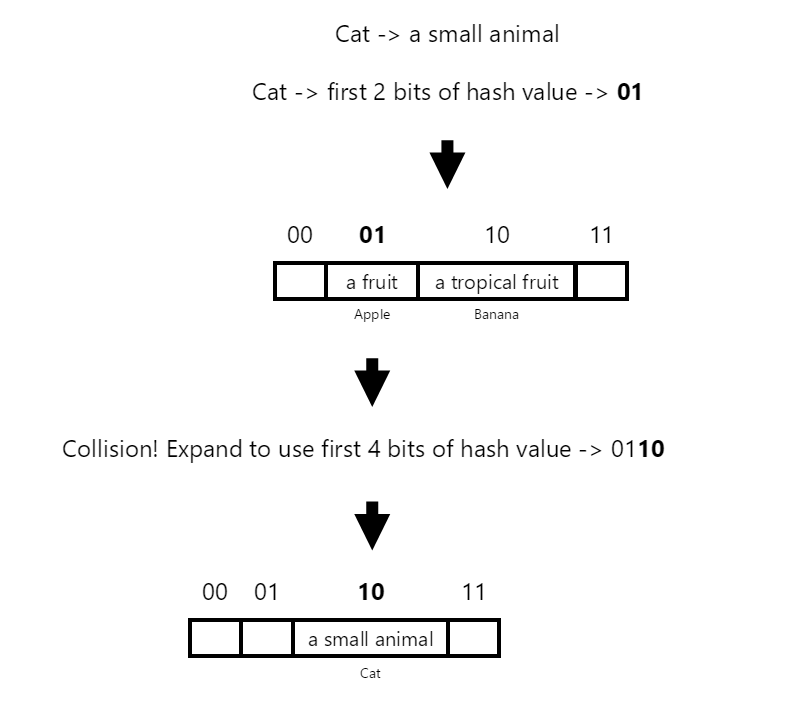
Finally, we insert "cat" -> "a small animal". The key is hashed, and the corresponding index is determined. Let’s assume that the first 2 bits of the hashed value for cat turns out to once again be 01 (the same value that we used for apple). We now have a collision!!
Normally, when the hash table gets big, we need to allocate a larger and bigger hash table and recalculate all of our hash values. This can be a slow and expensive process! Is there any way that we can avoid having to perform this step?
Well, this is where HAMTs come to the rescue!!
Instead of performing a resize on our table, we simply allocate a new hash table (which also has 4 empty slots) and we link our collision slot (01) to point to this new table:
Now, we can add “cat” to our second table, but we have a slight problem. We need to use more bits in order to obtain our hash value. In this instance, we simply use the 1st 4 bits instead of just the 1st two (which we used for apple and banana).
Let’s assume that the first 4 bits of our hashed value for “cat” map to 0110. We already used the first 2 bits (01) to try to index our value in our first hash-table. Now, we use the next 2 bits (3rd and 4th bits → 10) in order to index our element within our 2nd hash table:
The above methodology of hashing gets rid of the need for us to do re-hashing. If we continue like this, we can add as many values as we like without needing to allocate more memory.
To find a value, we first simply calculate the hash. We then look at the lowest two bits and go to the root table to try to find our value. If a value exists at that position and it matches our key, we return it. Otherwise, we know that that isn’t the value we were looking for so we continue with the next two bits and use those to find a reference in our second table and so on and so on.
In this way, the HAMTs efficiently handle collisions by using a trie-like structure within the hash array. In essence, they’re a combination of a binary search tree and hash table but without any of their annoyances. Binary search trees require for us to balance the tree every time we insert something due to the fact that we want to keep our search-paths logarithmic and efficient. In an HAMT, the positions are determined by the hash, so the positions will be more random and do not require balancing. As for hash tables, we already mentioned the annoyance of the needing to re-allocate more memory and to re-hash values in instances when our table is full. An HAMT never gets full due to the fact that it's a tree. In instances where we need to allocate a new value, we just continue adding more child nodes.
HAMTs are frequently used in functional programming languages, such as Clojure and Scala in order to implement persistent data structures like maps and sets. HAMTs provide efficient lookup, insertion, and deletion operations while ensuring immutability. They’re also well-suited for concurrent environments where multiple threads or processes access and modify shared data structures simultaneously. Their structural sharing property allows for efficient copying and sharing of data, reducing the need for expensive locking mechanisms.
Please note that this example provides a simplified explanation of HAMT's working principles, and actual implementations may involve more complex optimizations and details.
You can grok the other nuances and the various optimizations which are available within HAMTs by reading the excellent blog post linked below:
You can also find an excellent implementation of a HAMT in the repo provided below: