Grokking Huffman Coding

An intuitive and visual intro to Huffman coding.

Huffman coding is a popular method of data compression that's widely used in computer science. It was developed by David A. Huffman in 1952 while he was a Ph.D. student at MIT and its primary purpose was to efficiently represent data in a way that reduced its size – thus making it more efficient for storage or transmission. In essence, to provide efficiency, the more frequent data values are assigned shorter encodings while the less frequent ones are assigned longer ones.

Let’s go back to the beginning so we can provide an in depth analysis on exactly what Huffman coding entails.

Introduction

To represent strings using digital language, we need to come up with a scheme of encoding our letters and alphabet of characters into a sequence of ones and zeros which can be used to encode each letter in our alphabet. But how do we choose which binary representation to use for each one of our letters? Well, we could just randomize it such that a random and unique sequence of binary digits encodes a letter in an arbitrary fashion. As an example, we could just use the code ‘0’ to represent the letter ‘a’, ‘1’ to represent the letter ‘b’, ‘01’ to represent ‘c’ and so on and so on, but there are 2 big problems with using such a scheme!

Issue #1: Efficiency

For one, doing this wouldn’t be very efficient! Why? Well, we know that different letters of the alphabet occur at different frequencies, so instead of using a simple random assignment, it would actually make more sense to try to use a shorter binary encoding for letters which occur more frequently while giving the less frequent ones a longer one!

Let’s take a look at the relative letter frequency of each letter in the English alphabet:

Source: https://en.wikipedia.org/wiki/Frequency_analysis#/media/File:English_letter_frequency_(alphabetic).svg

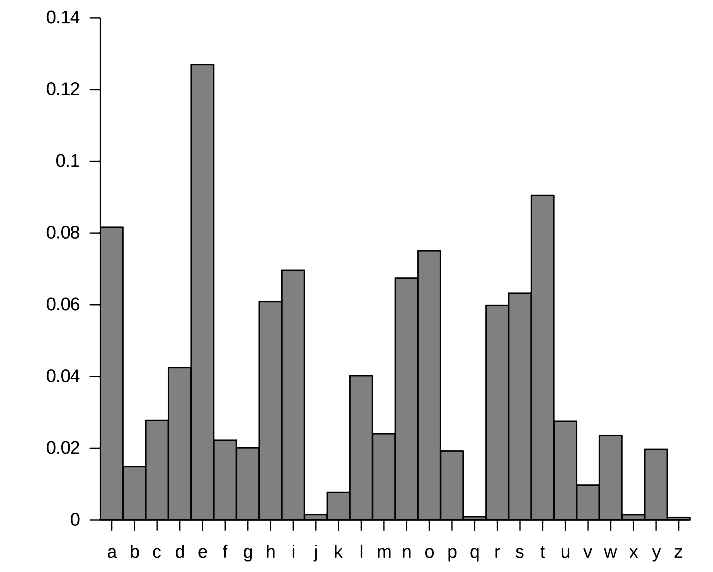
In the above example, we see that letters such as ‘e’ and ‘t’ occur much more frequently than letters such as ‘z’ and ‘x’. Knowing this, we should also be able to note that devising an encoding which represents the letter ‘e’ with a shorter encoding (such as ‘0’) and using longer encodings for less frequent letters such as ‘z’ would be a great thing to do! This way, we get an extremely efficient encoding of our string and we thus minimize the amount of information which we need to store / send!

Issue #2: Encoding / Decoding Ambiguity

We have another problem with using the scheme we illustrated above though. We can’t simply use a random assignment of binary digits to encode each letter. Assuming that we did, and assuming we used our original premise to encode a as ‘0’, b as ‘1’, c and ‘01’, d as ‘10’ and e as ‘11’ for example, if we had the binary encoding shown below:

Using sing our randomized encoding, we wouldn’t know whether it encoded ‘ababa’:

or whether it belongs to the encoding shown below (‘cad’):

In other words, if we’re not careful, our encoding could be interpreted in multiple ways, and we can’t have this level of ambiguity! So how do we mitigate this?

Well, we enforce a rule: we make our binary encoding prefix free. What this means is that no encoded letter representation can be the prefix of another encoded letter. This way, any encoding which we encounter is unambiguous, and leads to one translation and only one representation of our encoded string!

As an example, if we made our above a, b, c, d, e encoding a valid prefix encoding — we could represent each letter as:

In the above instance, no prefix is used in encoding any other prefix. Using the above encoding ensures that a string such as ‘1 0 1 0 1’ which we saw earlier can only be interpreted in one way:

Now that we know a technique to use to assign unique encodings to the letters in our alphabet, can we come up with an algorithm or scheme such that the most frequent letters in it are assigned to shorter strings, while the less frequent ones are longer?

Well — this is exactly what David Huffman devised in 1951! This is what we refer to as Huffman coding.

Huffman Coding

Huffman coding works by creating a binary tree which uses the leaf nodes to store our letters, while using the path from our root node to the leaf as the binary representation of the letter. Whenever we transverse our tree using a left child, we use 0, and whenever we transverse to the right, we use 1.

As an example, we can use the below tree to encode the first 3 letters of the alphabet:

In the above instance, the letters are encoded using the binary strings shown below:

How did we get the above representation? Well, as we already stated, we get our encoding by traversing down from the root node of our tree to the leaf node. Each time we encounter a left child, we add the binary digit 0, and each time we encounter a right child, we add a 1:

There’s more to it than this though. We now have to find a method of constructing such a tree in a manner such that our more frequent letters have smaller encoding lengths than the longer ones, so our job is not done!

Encoding Things Efficiently

We need to find a way to encode a message written in an n-character alphabet so that it’s as short as possible. In order to do this, we construct an array of letter frequency counts which we denote as frequency [1 … n] and then we need to now find a way of computing a prefix-free binary code such that it minimizes the total encoded length of the message, and so our optimization function can be described as:

where depth[i] denotes the encoding or tree length of the character at index i while frequency[i] denotes the frequency of this character within our string! More specifically, in order to achieve the objective which we’re trying to achieve - we need to minimize the above function! Doing so ensures that our encoding is efficient. Why?

Well, the larger the depth of our letter leaf node, the longer the encoding, so it’s clear here that our frequency will need to be small. Otherwise, we would get a huge sum assignment to this representation, and we wouldn’t be doing much in order to minimize our function. On the other hand, the larger the frequency, the lower our leaf depth will have to be. Here, we need to ensure that no large weights and encodings are used for letters which have a high frequency! Our function thus serves as a great optimization function: in order to get our optimum, we need to make sure that our lower depth nodes (represented with shorter binary encodings) are assigned to more frequently encountered letters, while the less frequent letters are assigned to leaf nodes which have a larger depth (and larger binary encodings).

This is where our Huffman coding algorithm comes in handy. To find an optimum for our function and encode a string in an efficient way, we use the simple methodology outlined below:

1. Build a letter frequency table which holds the frequency of our alphabet over the string we’re trying to encode.

2. Look at the table and find the 2 least frequent letters / nodes.

3. Merge them into one node such that the 2 nodes above are the children of the new node, and the total weight of this node is equal to the sum of the frequencies of the 2 child nodes.

4. Add the above node to our table, and continue repeating steps 2 to 4 until each one of the nodes in our table belong to our binary tree.

The above may initially look a bit complicated, but it’s actually very simple. Let’s take an example an illustrate how our algorithm builds an optimum tree.

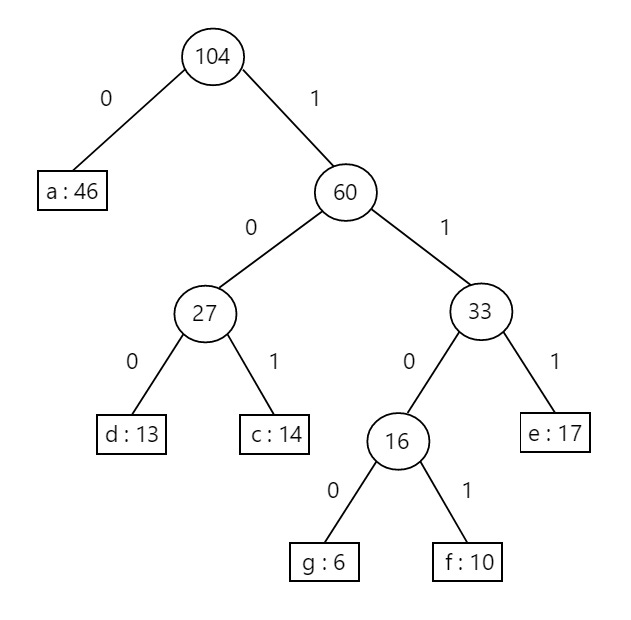
Assume that we have the letter frequencies shown below:

Let’s go ahead and build a Huffman tree.

First, we take the 2 least frequent nodes (g and f), merge them into a new node, and add the new combined node back into our frequency table, as illustrated below:

We then repeat the same steps: this time, we see that our least frequent nodes are letters d and c, and so we combine them and add them back to our table:

Once again, we take our least frequent nodes (our combined g and f node with a frequency of 16 and our e node containing a frequency of 17), combine them, and add them back to our ordered frequency table:

We now only have 3 nodes left! We no longer show the insertion step – now, we’ll simply show the merging step of merging our 2 least frequent nodes (27 and 33), resulting with an ordered node list composed of only 2 nodes:

Finally, we merge our last 2 nodes to get our final Huffman tree, with each encoding shown below:

Our final letter encodings are provided below, and we obtain them by traversing down from the root node to the leaf node encoding our letter / symbol:

We can also see that our encoded character length / depth are constructed such that the more frequent characters have a lower depth than the less frequent once. Look at our final table, it’s easy to see that our final tree gives us an optimal construction for minimizing our message length:

Our total cost of encoding this string using our Huffman construction is 24 + 40 + 39 + 42 + 51 + 46 = 242, which means that it will take us 242 bits to encode our original message using our tree construction! Is there a more efficient way of constructing our tree?

Surprisingly, no!!! Huffman coding always constructs an optimal prefix free binary code. This means that we can’t beat our above encoding of 242 bits – any tree we construct will always either take 242 or more bits to encode the original message. The reason for this is due to the greedy nature of our algorithm. In each instance, we make the optimal choice of combining the 2 least frequent nodes into one, and recurring onward and continually using the same methodology until we have our final tree. This ensures that the least frequent letters in our encoding are assigned to tree nodes which have the lowest depth, while the more frequent nodes are assigned to leaf nodes located deeper down our tree.

We won’t go into the formal proof, but it’s good to note that we can easily prove that our Huffman coding always provides with an optimal encoding length by showing that our tree construction always optimizes our original cost function which attempts to minimize:

We also note that in order to efficiently construct a Huffman code, we can keep the characters in a priority queue, and use the character frequencies as priorities, which ensures that our algorithm runs in O(nlog(n)) time.

Implementation

Let’s provide the code for constructing a Huffman tree using Python to finish things off. Below - we use a priority queue to construct our tree and print out the results after we’re done:

import heapq

class TreeNode:

    def __init__(self, name, priority):
        self.name = name
        self.priority = priority
        self.left_child = None
        self.right_child = None

    def __lt__(self, other):
        return self.priority < other.priority

    def print_huffman_codes(self, code=''):
        # Print the character and its Huffman code
        if self.name is not None:
            print(f"Character: {self.name} -> Huffman Code: {code}")
        if self.left_child:
            self.left_child.print_huffman_codes(code + "0")
        if self.right_child:
            self.right_child.print_huffman_codes(code + "1")

def build_huffman_tree(message):

    # Create a frequency map
    frequency_map = {}
    for char in message:
        frequency_map[char] = frequency_map.get(char, 0) + 1

    # Initialize a priority queue
    priority_queue = []

    # Create nodes for each character and push them into the priority queue
    for char, frequency in frequency_map.items():
        new_node = TreeNode(char, frequency)
        heapq.heappush(priority_queue, (frequency, new_node))

    # Build the Huffman tree
    while len(priority_queue) > 1:

        left_priority, left_node = heapq.heappop(priority_queue)
        right_priority, right_node = heapq.heappop(priority_queue)

        # Create a new tree node with combined priority
        new_tree_node = TreeNode(
            name=None,
            priority = left_priority + right_priority
        )

        new_tree_node.left_child = left_node
        new_tree_node.right_child = right_node

        heapq.heappush(priority_queue, (new_tree_node.priority, new_tree_node))

    # The remaining node in the priority queue is the root of the Huffman tree
    root = priority_queue[0][1]

    return root

# Example usage:
message = "This is an example for Huffman encoding -- the most common characters are encoded using the least amount of characters."
huffman_tree = build_huffman_tree(message)
huffman_tree.print_huffman_codes()

Using the example string we provided above (‘This is an example for Huffman encoding -- the most common characters are encoded using the least amount of characters.’) - we get the encoding provided below:

Character: e -> Huffman Code: 000
Character: r -> Huffman Code: 0010
Character: H -> Huffman Code: 001100
Character: l -> Huffman Code: 001101
Character: d -> Huffman Code: 00111
Character: m -> Huffman Code: 0100
Character: t -> Huffman Code: 0101
Character: s -> Huffman Code: 0110
Character: c -> Huffman Code: 0111
Character: u -> Huffman Code: 10000
Character: i -> Huffman Code: 10001
Character: n -> Huffman Code: 1001
Character: o -> Huffman Code: 1010
Character: f -> Huffman Code: 10110
Character: p -> Huffman Code: 1011100
Character: . -> Huffman Code: 1011101
Character: g -> Huffman Code: 101111
Character:   -> Huffman Code: 110
Character: T -> Huffman Code: 1110000
Character: x -> Huffman Code: 1110001
Character: - -> Huffman Code: 111001
Character: h -> Huffman Code: 11101
Character: a -> Huffman Code: 1111

It’s relatively easy to observe that our most common characters (such as ‘e’ and the space character) are encoded using the least amount of characters while the least frequent ones (such as ‘T’ and ‘x’) have larger encoding lengths!

In Sum

Isn’t it beautiful? Through such a simple and elegant algorithm, we can construct an optimal tree with minimal effort. In addition to having an easy to construct tree, our decoding process becomes extremely simple. In order to decode any message, we simply traverse down our tree until we hit a leaf node. When we do hit one, we know that our binary encoding represents the letter present in our leaf, and we continue on traversing down again from root to leaf, adding letters as we encounter each leaf node until we get to the end of our encoded string and we have our original / decoded message.

Huffman coding is a fundamental technology that underlies many aspects of our digital lives. It's instrumental in making data storage, data transmission, and various media formats more efficient, allowing us to work with and consume digital content more conveniently and economically. It's the foundation of file compression formats, facilitating the compression of documents, images, and videos. Moreover, it plays a crucial role in networking, data storage, audio compression, mobile communication, and various voice encoding technologies, contributing to faster and more data-efficient digital experiences.

Hopefully you found this overview helpful and you now understanding how Huffman coding works!