Intuitive Guide to Quick Sort
A guide to quick-sort focused in on providing simple visuals and intuition.
I recently posted and did an overview of the merge sort algorithm which you can find here.
Quick sort is very similar to merge sort. The main difference between the two lie in the approach they each use in sub-dividing the input space. Quick sort uses a more elaborate approach in deciding which group each input element gets partitioned into. Instead of simply dividing each group in half, quick-sort picks a pivot element which it uses to create a decision boundary. This boundary or element controls how our input elements are partitioned and we recursively keep dividing our groups until the product becomes extremely easy to merge in sorted order. Quick sort has the same major advantages that merge sort does with the addition that it tends to be faster on modern hardware architectures. Noting this, let’s dive into the quick-sort algorithm.
Basic Algorithm
The algorithm in its very essence is composed of the steps outlined below:
Pick a pivot element.
Partition the input into 3. To do this, we move non-pivot items to the appropriate side of the list, based on whether they’re less than or greater than the pivot value and we end up with:
First part: all elements in this part are less than the pivot.
Second part: contains the pivot itself.
Third part: all elements in this part are greater than or equal to the pivot.
Continue applying the sorting algorithm to the first and the third parts.
Join the first part, the pivot, and the second part.
A Simple Example
Let’s go through a simple example to explain how the algorithm works. Let’s say that I have group of industrial robots which are working at my factory. We’re situated in 2150 and Microsoft and its subsidiary OpenAI have taken over the planet. Human labor is no longer needed and factories are now run by robots. The robots are not all in uniform height though – they’re all different models, and the ‘security robot’ has at the front gate has been complaining about constantly raising the ramp for each robot coming through the gate.
To remedy this – the plant manger decides to come up with a plan: instead of letting each individual robot exit the premises individually, he figures that if he sorts the robots from smallest to tallest, he can simply get them to all line-up and march towards the exit. If he gets them to march together with the smallest robot being at the front and largest at the back, the ‘security robot’ then just has to steadily raise the gate as the lined up bots march on through. Once that last tallest robot walks by – the security bot can lower the ramp. We are thus only raising our exit ramp once instead of having to raise it multiple times for each bot. This results in great energy savings and an amazing return in shareholder value!! Microsoft execs would indeed be very happy when reporting this to the CEO up at the head office, so they give the initiative a big thumbs up!
But how do we come up with a sorting plan and how do we instruct the robots to line-up without having to complicate too many things?
Well – we could simply use the merge sort algorithm, which looks very simple and should be easy to execute, but the plant manager decides to come up to a different scheme. He knows that these robots love recursion – so he decides to give them instructions as a recursive formula and in the following manner:
All right boys, I need you all to pay attention. We need to all line-up, but the line up needs to be in sorted order. To be in sorted order, you all need to follow these instructions.
First, pick a random robot out of the group. We will call this robot ‘pivot-bot.’
Once pivot-bot is picked, I want it to move into the middle of the room.
Once this is done, you all need to figure out which side of pivot-bot to go to, and this will be decided by looking at pivot-bots height.
If you are shorter than pivot-bot, please line up to the left. If you are taller than pivot-bot, you need to go into a group located on the right.
Got it?
Great. Once you’re finished partitioning into different sub-groups, you all need to repeat the steps I outlined above for each of the sub-groups we just created (i.e. both the left and the right sub-groups need to execute the above instructions again)!! We will call each of our resulting sub-groups partitions, with the left subgroup and right sub-group belonging to its own sub-partitions.
Keep executing these instructions until each of the resulting sub-groups are only composed of one robot (i.e. one element) and we can no longer create further partitions.
An example diagram showing this procedure is illustrated below:
We’re not finished quite yet though. We need to join these groups / partitions now.
Once there are no more sub-groups to partition – I want each sub-group to merge together from left to right. The partitions will keep merging until we have all of the robots standing next to each other and until we have one master-partition containing all of our robots.
Here’s another diagram which illustrates the merge procedure:
The plant manager sits down and watches this process takes place. It’s simple and it involves simple programming for our robots. There’s not much to remember here. The robots just recursively follow the same procedure over and over again until we get to our base case (we only have one robot left in our group). The merging process is extremely simple as well – the instructions are exactly the types of instructions robots are great in executing!!
In Place Quick-Sort
The plant manager is happy, but something seems off. First off, the sorting mechanism works and the robots end up being in sorted position, but something still seems off. He things to himself – hmm, it looks like there is a LOT of robot movement when we execute this procedure. Is there any way we can make this more energy efficient? In other words, is there a methodology which we can use to not make these robots move so much?
So, he sits down and takes a look at the original algorithm. After sketching it out and thinking carefully about it, he decides to take a little break and finds a video of a Hungarian folk dance which strangely resembles the process he was just thinking about:
That’s it, he says!!
After sketching it out and thinking carefully, he devises another ingenious methodology of programming his robots: instead of picking a random ‘pivot-bot’ and making him/her move to the middle of the room and then making each robot compare themselves to the bot and making each robot move to one side, the manager comes up with an ingenious plan:
All right bots, plan b. Instead of using a ‘random’ bot to pick out of each sub-group or group, we’re going to simplify things. Instead of using randomization, we’re simply going to use the first bot as the ‘pivot element’ or pivot-bot from each group.
Got it?
Now, instead of moving each pivot-bot to the center of the room and sub-dividing into 2 groups, I want each one of you to stay in the same position you’re currently located in and to follow the instructions I provide below:
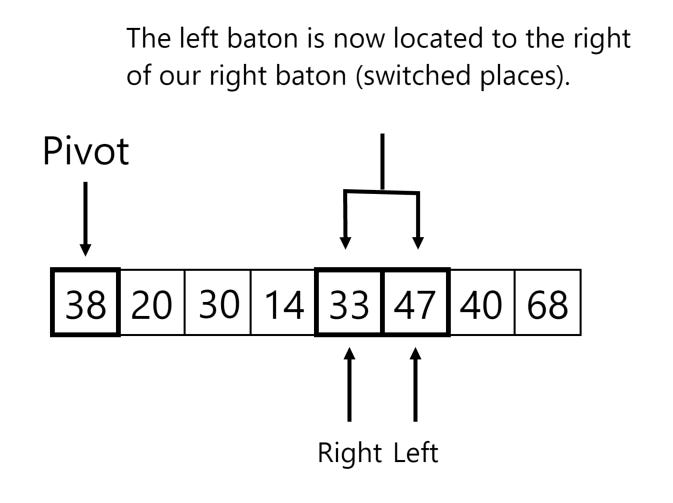
We’re going to pass a baton to the left-most bot in the group (the 2nd bot) and the right-most bot (last bot) in the group which are located to the right of our pivot-bot. Let’s label the left-most bot ‘left’ and right-most bot ‘right.’ Let me draw a simple visual so that this is easy for you all to see (each integer below represents a robot’s height):
We’re going to move each baton in a step by step manner and use the procedure below:
If the robot on the left side is smaller than our pivot-robot (the first robot in the group) – I want you to keep passing the baton forward to the next bot. You’ll keep doing this until you encounter a robot which is larger than our pivot-bot.
If the robot on the right side is larger than our pivot-bot – I want you to keep passing your baton to the left until you encounter a bot which is smaller than our pivot bot.
Now – assuming that the left baton is still on the left of the right baton, I want each robot with the left baton to exchange places with the bot carrying the right baton (and you’ll also exchange your batons as well!!).
Now, I want you to pass each baton to the bot ahead of you. I want you to keep repeating the above procedure as long as the left baton is still located to the left of the right baton.
If the left baton is to the right of the right baton (or if one robot is holding both batons), I want the robot holding the baton(s) located to the left to exchange places with the robot located at the pivot point.
Now, I want you bots to recursively repeat the same procedure for the group located to the left of the pivot element and for the group located to the right of the pivot as well. You’ll keep repeating the same procedure until all bots are sorted.
You should be able to notice two primary things from the procedure outlined above.
Once we move our pivot-bot and make it exchange places with the robot holding the left-most baton, both of our sub-groups are partitioned such that the left-group contains all of the elements less than the pivot while the right-group contains all of the elements larger than our pivot.
We didn’t need to use an elaborate procedure in moving our robots. Whereas in our previous procedure, we had to allocate extra space for our pivot-bot to move to the middle of the room, we now avoid moving our elements and simply use a ‘baton’ or ‘pointer’ to partition each sub-group. Whenever we find elements which are ‘out of order’ - we simply ask our baton-holding bots to swap places and continue.
Noting the cost-savings in terms of space and movement, the manager inserts the new program into each bot and tests out the new procedure. He notes down the improved energy and space efficiency. He gloats once again about his divine optimization abilities and calls the head-office to announce more great news!
Of course, there are many other ways of accomplishing the above procedure. The reason we chose the above steps and illustrations was to introduce the concept of doing an in-place version of quick-sort. We also chose to use the first element as our pivot and this introduces issues when it comes to already sorted elements. Ideally, we want to choose a pivot element in a random manner. Each pivot should have around the same amount of elements located to its left side as the amount of elements located to its right. Choosing our pivot in this fashion plays an important role in making quick-sort efficient at doing what it does.
Either way, you should now at least have a good mental intuition of how the in-place version of this sorting algorithm works and why it works as well as it does. Instead of iteratively moving each element from each sub-group into a separate region of memory, we’re essentially now doing things in place and ensuring that our algorithm doesn’t require any extra ‘space’ in order to perform each sub-sort!
Implementation
Below is a very simple implementation of quick-sort in JavaScript (not in-place):
// Function to return a random element from the given list
function random(list) {
return list[Math.round(Math.random() * (list.length - 1))];
}
// Function to perform quicksort on a given list
function quickSort(list) {
// Base case: If the list has 0 or 1 elements, it is already sorted
if (list.length < 2) {
return list;
}
// Choose a pivot element randomly from the list
const pivot = random(list);
// Partition the list into three arrays: elements less than, equal to, and greater than the pivot
const less = list.filter(i => i < pivot);
const equal = list.filter(i => i === pivot);
const greater = list.filter(i => i > pivot);
// Recursively apply quicksort to the two partitions and concatenate the results
return [
...quickSort(less),
...equal,
...quickSort(greater)
];
}
// Example usage:
const myArray = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5];
const sortedArray = quickSort(myArray);
console.log(sortedArray);
// [1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]For an in-place version, you can take a look at the implementation provided below:
// Function to perform quicksort on an array (in-place)
function quickSort(array, left = 0, right = array.length - 1) {
// Check if the array has more than one element
if (left < right) {
// Partition the array and get the pivot index
const pivotIndex = partition(array, left, right);
// Recursively apply quicksort to the left and right partitions
quickSort(array, left, pivotIndex - 1);
quickSort(array, pivotIndex + 1, right);
}
}
// Function to partition the array and return the pivot index
function partition(array, left, right) {
// Choose the pivot (for simplicity, using the rightmost element)
const pivot = array[right];
// Initialize the index to track elements less than the pivot
let i = left;
// Loop through the array to rearrange elements based on the pivot
for (let j = left; j < right; j++) {
if (array[j] <= pivot) {
// Swap array[i] with array[j]
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Move the index for elements less than the pivot
i++;
}
}
// Swap the pivot with the element at index i
const temp = array[i];
array[i] = array[right];
array[right] = temp;
// Return the pivot index
return i;
}
// Example usage:
const myArray = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5];
quickSort(myArray);
console.log(myArray);
// [1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]Advantages and Disadvantages
Let’s go over some advantages of using quick sort over merge sort:
Quick sort is usually faster than merge-sort.
It has better cache-locality than merge-sort.
Uses less memory than merge sort (if implemented correctly).
Some disadvantages of choosing quick sort over merge sort:
Merge sort is stable by design (equal elements keep their original order) while quick sort is not.
Merge sort is more parallelizable than quick-sort (i.e. better for multi-threading and distributing compute).
Merge sort uses (about 25%) less comparisons than quick-sort.
Quick sort’s worst case performance (O(n2)) is worse than the worst case performance for merge sort (O(n log n)).
Overall, both quick sort and merge sort and fantastic algorithms and each have their own advantages. Quick sort tends to be used more often in the real world due to its better overall performance than merge sort on normal workloads. This performance advantage is mostly due to cache-locality.
Cache-locality refers to the micro-processors ability to fetch information / memory blocks in an efficient manner by keeping them close to the CPU. RAM usually tends to be fast, but an L1 cache for example is 100-fold faster than RAM - so keeping information within the L1/L2/L3 cache regions and next to the CPU often pays off. Quick sort takes advantage of this locality and thus executes faster for non-giant data-sets. There are many other nuances and complexities to locality which I won’t get into here, but hopefully you found the above explanations and overview helpful! If you liked this write-up, make sure to like and subscribe!