Sorting algorithms are fundamental to computer science, and for a good reason: they’re used almost everywhere and play a huge role in optimization by making data organized. They also serve as a building block to many other complex algorithms. So, what are some of the key algorithms which are used when it comes to sorting?
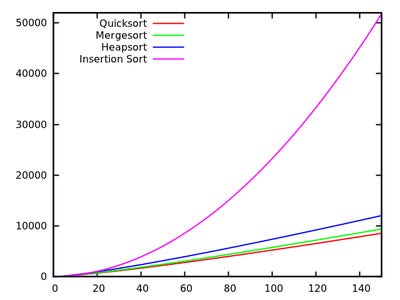
To answer this question, we need to focus in on the speed. Let’s take a look at what Knuth says about the various sorting algorithms and their run-time performance in his famous book series “The Art of Computer Programming” (Volume 3):
These results indicate that quick-sort is fastest, but it only applies to Knuth's artificial computer! In the real world, things tend to get a lot more complicated. I don’t have time to cover all the nuances, but this post covering branch prediction (or misprediction in this case) does a fine job in showing how modern processors may not handle things as simply as we may perceive them to do:
Note also that the algorithms relate differently for small inputs. Here is a comparison of our previous algorithms for inputs of only a few items:
In other words, the smaller our input, the less it matters which algorithm we choose! The differences really do matter though when it comes to sorting large data sets like those which we can find within a large database table, so choosing the right sorting algorithm really does play an important role in the real world!
Noting this, let’s start off by explaining and going over the merge sort algorithm!
Merge Sort
Merge Sort is a divide and conquer sorting algorithm which works by recursively breaking down a problem into two sub-problems of the same and related type. This process continues on until the two sub-problems become simple enough to be solved directly. The solutions to the sub-problems are then combined (or merged) to give a solution to the original problem.
You can think of it as the ultimate divide and conquer strategy. Let’s use an example to explain the entire procedure. Let’s say that you have a line up auditioning for a play, and you need to prioritize shorter people rather than taller people. The role involves some sort of gig which starts our with a short people joke, so the directors wanted to try to make sure that the selection process prioritized shorter actors. They asked you to sort the line up based on height, but you’re extremely anti-social, and you don’t even have the organizational skills to handle task of that magnitude! Instead of going through the line up and telling each individual which position to move to based on their height, you instead devise an ingenious plan. The instructions you give to the entire group are written and they go as follows (I’ve also included a sample diagram using integers (instead of actors) illustrating the process to help readers out):
‘All right guys (you say), I want you to split in half.
If there are more than two people within your new group, or sub-group, you need to repeat this same step, and continue splitting the group in half.
Keep doing this until you have two or less than two people within your group.
If you do have two people left, I want you to stand behind the person in your group if you happen to be taller than them.
If you’re shorter, I want you to stand in front of them.
After you finish re-arranging yourself in this manner, I want you to line up in this order and merge back into the original group you split from. When you do merge back into a new group, I want you to use this procedure in determining which person to merge first into our new line-up: pick the smallest person from each group. In other words, if the person at the front of group one is smaller than the person at the front of group two, make sure that the person in group one goes first! Keep repeating this step until your two groups are combined together and fully merged into one.
Using the above procedure ensures the our newly merged groups will be in sorted order, so it’s important that you keep using this procedure!
Understood?
Great! You need to keep merging your groups using the above steps until you have only one group left. Once you finish merging, we will use this new order for auditioning for our play.’
The above ensures that the new line up is in sorted order, and that your divide and conquer strategy keeps things simple: instead of having to keep the whole group order in mind, you sub-divide the group until you reach small enough groups where the actors can use a simple procedure in deciding how to re-arrange themselves using height as a comparison point. The merging process then ensures that the newly formed line ups give priority to shorter actors, and it’s simple enough to be followed without you having to intervene. You simply tell each sub-group to merge into a new group by continually picking the shorter actor from each group being merged. This ensures that our ordering property holds when combining our groups into one, and you’re pretty much set! Using the simple instructions above, if the actors follow the procedure, the final line up will be in sorted order!
Algorithm
Let’s outlined the algorithm steps more formally. Let’s say that as input, we have an unsorted list which we need to sort. In order to sort the list using our merge sort procedure:
We check if there’s only one element in our list. If there is, it is already sorted, so we return the one element.
If there’s more than one element, divide the list recursively into two halves until it can’t be divided anymore.
Merge the smaller lists into new list, making sure that each of the combined products is in sorted order when merging the 2 sub-lists.
A full visual illustrating a marge-sort process is also provided:
JavaScript Implementation:
// Split the array into halves and merge them recursively
function mergeSort(array) {
if (array.length === 1) {
// Return once we hit an array with a single item
return array
}
// Get the middle item of the array rounded down by creating a variable
const middle = Math.floor(array.length / 2)
const left = array.slice(0, middle)
const right = array.slice(middle)
return merge(
mergeSort(left),
mergeSort(right)
)
}
// Compare the arrays item by item and return the concatenated result
function merge(left, right) {
let result = []
let indexLeft = 0
let indexRight = 0
while (indexLeft < left.length && indexRight < right.length) {
if (left[indexLeft] < right[indexRight]) {
result.push(left[indexLeft])
indexLeft++
} else {
result.push(right[indexRight])
indexRight++
}
}
return result.concat(left.slice(indexLeft)).concat(right.slice(indexRight))
}Conclusion
The most important part of merge sort is its performance guarantee which is O(n*log(n)) — the highest performance we can get out of a sorting algorithm. Regardless of the original ordering of the input, we will always get very strong performance. There are no adversary test cases which can make it run much longer than this run-time, which is fantastic! Merge sort is therefore very suitable for sorting extremely large number of inputs!
Another advantage is that merge sort is considered to be a stable sorting algorithm. This means that the same elements in an array / list maintain their original position with respect to each other — so if we want to keep the elements within our original collection relatively ‘stable’ - we should choose merge sort over other algorithms.
Some not so great properties of merge sort?
Well, some people say that it is actually not so easy to implement from scratch (although I personally tend to disagree). The second one is that it requires additional O(n) storage during merging operation. It’s thus not very memory efficient and not in-place.
In Sum
Hopefully you found this intro and overview helpful, and I hope you stay tuned for our next sorting algorithm — the one and only and the king of all sorting algorithms: quick sort!!








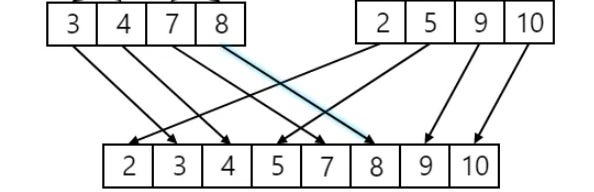

There is another version of mergesort which is not recursive, and may be easier to explain: do it bottom-up instead of top-down.
Go through the array, merging adjacent lists of length 1 into lists of length 2.
Then merge those adjacent lists into lists of length 4.
Then again into lists of length 8.
Etc.