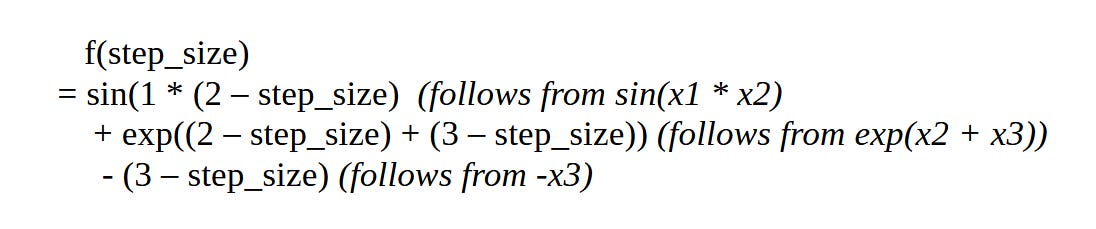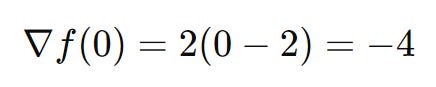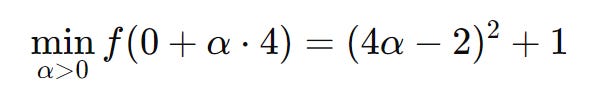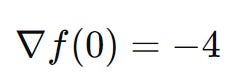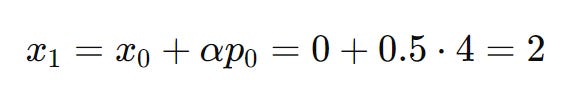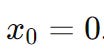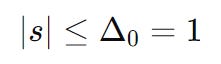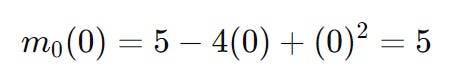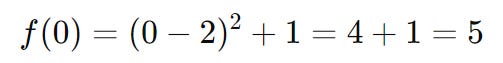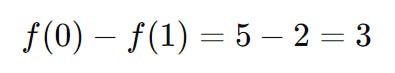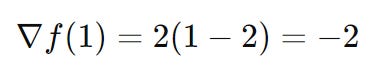Algorithms for Optimization (Explained Simply): Part 2 - Line Search and the Trust Region Method
A visual-focused and intuitive overview of important optimization algorithms. This blog post focuses explaining the details behind the line search and the trust region method.
Let’s continue on with our overview and series focused on optimization algorithms. If you haven’t read part 1, I highly recommend you go through it since it introduces some key concepts which we’ll need to familiarize yourself with in order to understand this section. Once again, a lot of this content is inspired by the book Algorithms for Optimization which I highly recommend.
In this section, we’ll go over some key algorithms which actually use local models (like the derivative) to incrementally improve a design by making small adjustments. We start with methods that pick a direction to move in (based on local information) and then decide how far to move.
Line Search
Line search method is an iterative approach of finding a local minimum which basically:
Chooses a direction to step into. Since we are searching for a minimum, this is a descent direction and we compute it using local gradient / derivative / Taylor approximation values of our function.
Chooses an appropriate step size to move into.
Repeats steps 1 and 2 until the terminal conditions are met (i.e. we are close or at a local minimum & the derivative or gradient vectors are close to 0).
That’s pretty much it. Although some implementation details will differ (like computing our direction / step size) – the gist is basically the same. All we’re doing is using local information to compute appropriate step sizes and directions and walking into these directions.
Knowledge Review
Taylor Approximation:
A Taylor approximation is a way to estimate the value of a function near a specific point using the derivatives or derivative values located close to that point. It's basically using the local properties of an area around a function point to approximate the shape of the actual function. The key steps for this are outlined below:
Pick a point p where you want to approximate the function.
Use Derivatives: Use the value of the function and its derivatives at that point to create the approximation.
Build the Polynomial: Combine these values into a polynomial. The more terms (derivatives) you use, the better the approximation.
You can find a great intuition and explanation of Taylor series here (courtesy of 3Blue1Brown / Grant Sanderson):
Gradient:
The gradient is the generalization of the derivative and gives us the direction of steepest increase of a function. In the instance of a scalar function shown below:
The gradient plotted over its surface is:
The gradient of f at x is written ∇ f(x) and each component of the resulting gradient vector is the partial derivative of f with respect to that component:
In the above instance, we’re simply computing the partial derivative of x with regards to its variables and putting it in vector form. Once again – this give us a directional vector which points in the direction where the function increases most (which we can also denote as the ‘steepness’ of the function). To approach a minimum or downward direction, we simply have to follow take the opposite vector – another great example showing the gradient of a 2-dimensional function (a function composed of 2 independent variables) is provided below:
Python Based Example
Let’s get back to our line-search algorithm and outline a simple example which will show us the details of how line search can be implemented (using Python).
The function which we will attempt to minimize is provided below:
The position we want to start on is (1, 2, 3) and our direction is [0, -1, -1].
Let’s start off by writing some Python code:
import numpy as np
# Define the original function
def original_function(x1, x2, x3):
"""Original function to minimize, given three variables."""
return np.sin(x1 * x2) + np.exp(x2 + x3) - x3
# Initial point and direction
initial_point = np.array([1, 2, 3])
direction = np.array([0, -1, -1])Next, let’s redefine our original function into a single parameter optimization based on a computed step size and direction. To do this, we simply substitute our initial (x1, x2, x3) values (1,2,3) and sub in an appropriate step parameter for each one of our 3 independent variables (which will once again be in the step direction [0, -1, -1]). Our new objective function will be:
We can determine the re-parametrized values of our (x1, x2, x3) variables which will now be:
We sub in these values to get:
We can simplify the above to get:
Converting the above into python we get:
# Define the simplified objective function
def simplified_objective(step_size):
"""Objective function to minimize with respect to the step size."""
return np.sin(2 - step_size) + np.exp(5 - 2 * step_size) + step_size - 3Finally we define our line search function and use it to find the optimal step size and our the minimal value present at this step:
# Line search algorithm
def line_search(original_func, initial_point, direction):
# Define the objective function for line search
def objective(step_size):
# Compute the new point based on alpha and direction
new_point = initial_point + step_size * direction
# Returns a scalar by evaluating the original function at the new point
return original_func(new_point[0], new_point[1], new_point[2])
# Minimize the objective function
from scipy.optimize import minimize_scalar
result = minimize_scalar(objective)
optimal_step_size = result.x
# Compute the new point using the optimal alpha
new_point = initial_point + optimal_step_size * direction
return new_point, optimal_step_size
# Perform line search
new_point, optimal_step_size = line_search(original_function, initial_point, direction)
# Print the results
print(f"Optimal step_size: {optimal_step_size}")
print(f"New point after line search: {new_point}")
# Verify by evaluating the function at the new point
new_function_value = original_function(new_point[0], new_point[1], new_point[2])
print(f"Function value at new point: {new_function_value}")The final result which we get when we execute this is:
which is as expected.
Another Example
The above example may be a bit-convoluted for anyone not familiar with Python or programming, so let’s go through another example which is simpler and which doesn’t use any code.
Let’s say that we want to minimize the following function:
Step 1: first, we need to choose our initial point. Here, we’ll start with 0:
Step 2: We choose a search direction (which we label as pk). In this case, we can use the negative gradient as our search direction (since we’re trying to minimize our function and the gradient points in the steepest direction). We can obtain the gradient by taking the derivative of our original function f(x) = (x – 2)2 + 1 which results in:
At x0, the gradient is:
So, since we want to negate the gradient we get -(-4) = 4 and he search direction is:
Step 3: Perform a line search to find the step length (which we denote as α). To do this, we have to solve the problem of finding the step length α that minimizes:
This means solving:
We can expand and simplify the expression (by subbing in 4α into our x variable) and we get:
Now, we take the derivative of this with respect to our step length (α) to find the minimum:
Setting the derivative equal to zero to find the critical point:
We now know that our optimal step size is 0.5.
Step 4: Update the next iterate / point (which we denote as x1):
Step 5: Repeat the process. At x1 = 2, the gradient is:
Since the gradient is 0, we know that we’ve found the minimum and we are finished.
Our 2 examples both used derivative information to come up with exact step-sizes, but in practice, you would approximate the step length rather than solving it exactly. You could do this by using trial values until you find a good enough reduction in the function. This is where the approximate line search algorithm comes in handy.
Approximate Line Search
It is often more computationally efficient to perform more iterations of a descent method than to do exact line search at each iteration, especially if the function and derivative calculations are expensive. Approximate line search gives us a way to move in the correct direction without overshooting or undershooting too much. This is done without having to calculate the optimal step size. It does this by finding a good enough step size quickly and by steadily moving towards our goal.
A general intuition for this algorithm can be obtained by imagining that you're blindfolded and trying to walk downhill. You can't see the whole slope, but you can feel with your feet whether you're going up or down. You take careful steps, feeling the ground, and stop when you feel like you've reached a point where going further might make you start going uphill again. You may ask yourself though: how do we calculate our step size using the above approach?
Well, this is where backtracking line search comes in handy: when you’re walking down the slope, you take a big step – but prior to doing so, you check if the step size takes you to a point which decreases your elevation by a sufficient decrease (i.e. your elevation or objective function must go down by a conditional value). If it feels like you might have overshot, you take a smaller step and try again until you find a step that feels just right. To be exact, in the algorithm:
You begin by taking a large step in the direction that you believe will reduce the function's value.
After taking the step, you check if the function's value has decreased enough compared to the starting point.
If the decrease isn't sufficient, you reduce the step size (by multiplying it by a constant less than 1) and try again.
You continue this process, reducing the step size each time, until you find a step that gives a satisfactory decrease in the function's value.
The algorithm outlined in Python is provided below:
def backtracking_line_search(f, grad_f, x, descent_direction, max_step_size, reduction_factor=0.5, wolfe_condition_param=1e-4):
y = f(x)
gradient = grad_f(x)
# This gives rate of change of function in the direction of the descent.
while f(x + max_step_size * descent_direction)
> y + wolfe_condition_param * max_step_size * (
# Dot product between the gradient and the descent direction
gradient @ descent_direction):
max_step_size *= reduction_factor
return max_step_sizeBacktracking Line Search Example
Let’s go through an example to illustrate how our backtracking algorithm works by using the same example which we overviewed for our regular line search algorithm. The function which we are aiming to minimize here is provided below:
Step 1: Choose an initial point x0. Here - we’ll once again use 0:
Step 2: Choose a search direction pk. Here, we’ll once again use our negative gradient information (from our earlier example) and to get 4 as our direction:
Step 3: Perform backtracking line search.
Backtracking line search involves choosing an initial step length α (usually α = 1) and then reducing it by multiplying by a factor β (e.g., β = 0.5) until a sufficient decrease in the function value is observed.
Parameters for backtracking line search:
Initial step length α0 = 1.
Reduction factor β = 0.5.
Condition parameter c = 0.5.
We want to find the largest step length α such that the function value decreases enough. Specifically, we want α to satisfy:
This condition ensures that the new function value is smaller than the current function value, but by at least a fraction of the step size.
Step 3.1: Evaluate the function at α = 1. First, we compute f(0 + 1⋅4) = f(4). The function value at x = 4 is:
Next, we check if this satisfies the backtracking condition:
Since 5 is not less than -3, we need to reduce our step length.
Step 3.2: Reduce the step length by β = 0.5.
First - we evaluate:
Next, we check our backtracking condition:
Since 1 is less than or equal to 1, our condition is satisfied!
Step 4: Update the point x1 to once again obtain 2 (which is our minimal point):
Step 5: Repeat the process. This is similar to our original line search. Since we know that our gradient at x = 2 is 0, we know that we’ve found the minimum and we end our search.
This ends our example. Hopefully you understand why the line search algorithm is so powerful. Next, we’ll overview an algorithm which is called the trust region method. The key advantage of this method over backtracking or regular line search is its ability to adaptively control the step size by constructing a local quadratic model of the function. This helps handle highly nonlinear or irregular functions more effectively.
Trust Region Method
Descent methods can sometimes place a bit too much trust in first or second order information, which can result in extremely large steps / premature convergence. The trust region method avoids this by limiting the step taken and trying to predict the improvement associated with the step and comparing it with the actual improvement. This local ‘predictive’ model or local landscape we tend to call the trust region. If our predicted improvement is accurate, we expand this trust region –- otherwise, we know that our local model is inaccurate so we shrink / contract it. Trust region methods first choose the maximum step size and then the step direction, which is in contrast with line search methods which first choose a step direction and then optimize the step size.
A good intuition for this algorithm is to imagine that you're walking through fog in a hilly area, trying to find the lowest point. Instead of picking a certain direction and attempting to take a step, you first try to create a local model of the area that’s directly around you. To check if your internal mental model matches reality, you take a small step within that local area and if the predicted elevation doesn’t match what you think is there – you ‘shrink’ the step size and keep repeating this process until you have a good mental image of the area surrounding you. Once your prediction does match the outcome, you then pick the appropriate direction and move towards it. After all - you don't want to make big, risky leaps because you can't see far ahead. Instead, you take careful, small steps within an area you feel confident about. If the ground seems to be sloping downward nicely and matches your internal mental model, you might get more confident and take larger steps. But if you stumble or the ground feels uncertain, you shrink your steps and proceed with more caution.

The heuristic steps used in this algorithm are provided below:
Start with a Guess: You begin at an initial guess for the solution. This is like starting at a certain point on a hilly landscape if you’re trying to find the lowest valley.
Define a Trust Region: Around your current guess, you define a small region (like drawing a circle around yourself). This region is called the "trust region." The idea is that within this small area, you trust that the function behaves somewhat like a simpler model (often a quadratic function).
Optimize Within the Trust Region: You look for the best direction and step size to move within this trust region. This is like carefully walking within the circle to see if you can find a lower point.
Check and Adjust:
If the move you make within the trust region significantly improves your position (i.e., lowers the function value), you trust the model more and possibly expand the trust region to allow for bigger steps.
If the move doesn’t improve much or makes things worse, you shrink the trust region and take smaller steps.
Iterate: You repeat this process—moving, checking, and adjusting—until you find the minimum or maximum value you’re looking for.
Let’s go through an example to illustrate how the trust region method works.
Trust Region Method Example
Let’s use the same example we used in our prior 2 algorithms / methods. Once again, we’re trying to minimize below:
Step 1: Choose an initial point x0.
Here we once again use 0:
Step 2: Set up the trust region.
The trust region is a region around the current point within which we trust a quadratic approximation of the function. We'll assume an initial trust region that has a radius of 1:
Step 3: Construct a quadratic model of the function.
For trust region methods, we approximate the objective function using a quadratic model. The quadratic model at x0 is based on the Taylor expansion of the function around x0:
For our original function, we know that the gradient (derivative is):
To obtain the Hessian is rather easy - we simply take the derivative of our above function (2x - 2) and we get a constant (2 — since the derivative of 2x is exactly 2):
At x0 the gradient is:
So, subbing this into our original quadratic equation gives us:
Fantastic!! We can now use this model for our next step!
Step 4: Minimize the model within the trust region.
We minimize the quadratic model m0(s) but subject to the constraint that the step size (s) must lie within the trust region. The trust region constraint is:
We now minimize the quadratic model we obtained earlier (i.e. 5 − 4s + s2), and we do this by simply taking its derivative:
Setting this equal to zero gives the critical point:
However, this step is outside the trust region since our we defined this region to be a equal to 1 (in step 2). In other words - we cannot take a step size of 2 so we simple take a step defined by our boundary and simply set s = 1 instead.
Step 5: Evaluate the new point.
At s = 1, the new point is:
The function value at x = 1 is:
Step 6: Adjust the trust region.
Now, we check whether the quadratic model predicted the function value accurately. The predicted reduction in the model is:
At s = 0 we have:
At s = 1 we have:
The predicted reduction there for is simply the difference between these two, so its equal to 5 - 2 = 3.
And - checking this by actually subbing in these values into our real function we get:
Since the model accurately predicted the reduction (3 = 3), we can increase the trust region radius for the next iteration. Let’s increase our step radius to now equal to 2:
Step 7: Repeat the process.
At x = 1, the gradient is:
We also know that the Hessian of our function is equal to 2 - so regardless of the input, the Hessian of our value is still equal to 2:
Knowing these 2 values, we can construct our new quadratic model:
This is the quadratic model we will use for x = 1. We need to minimize this function in order to get our next step — and once again, in order to do this, we take the derivative and set it to 0 to find the critical points:
The next step size (s) is equal to 1, and since this falls within our trust region (the size is smaller than 2) — we can proceed with evaluating our next point. We know that x1 = 1 and we sub this in to get our next x value:
The function value at this point is:
We can see that the above method leads us to our minimum (x = 2) in only two iterations.
The main difference between this method from and the approximate line search is that in this case, we only moved as far as the model was trustworthy and adjusted the region size dynamically based on the model prediction accuracy. Unlike approximate line search, which adjusts step lengths along a search direction through trial and error, the trust region method adjusted the step size in a much more calculated way. This methodology of adjusting the step size usually leads to more robust convergence, especially when dealing with complex functions or poor initial search directions. It balances making progress toward the solution while avoiding risky or uncertain moves.
This ends the outline for our algorithms — in the next section, we discuss some key methodologies which are used in deciding when to terminate our algorithm(s). Up until now, we assumed that we had a clear cut answer, but in the real-world, things tend to be a bit more complex.
Termination Conditions
There are four common termination conditions for descent direction methods:
Maximum Number of Iterations: This is a practical condition that stops the optimization process after a predetermined number of iterations, even if the other conditions haven't been met. This is useful for preventing the algorithm from running indefinitely, especially in cases where convergence is slow or uncertain.
Absolute Improvement (i.e. small change in objective function value): This condition monitors the change in the value of the objective function (the function you're trying to minimize or maximize) between iterations. If the change is very small, it suggests that further steps are unlikely to significantly improve the solution. A small change in the objective function value indicates that further iterations aren't making meaningful improvements, so the process can be stopped.
Imagine that you're iteratively adjusting a recipe to get the perfect taste. After several tweaks, the taste changes very little with each adjustment. At this point, you decide that it's "good enough" and stop making further changes.
Relative Improvement (i.e. small step size): This condition checks if the step size taken in the descent direction is very small. If the algorithm is only making tiny steps, it might mean that the function is nearly flat around the current point, and significant progress isn't possible.
A great intuiting for this is imagining that you’re adjusting a thermostat to find the perfect room temperature. Eventually, you find yourself only making tiny adjustments and realize that the temperature doesn't change much with each tweak, so you know you're already close to the ideal temperature and you stop adjusting.
Gradient magnitude: This condition checks whether the gradient of the function is close to zero. The gradient represents the direction and rate of the steepest ascent. In descent methods, we move in the opposite direction (downhill), so if the gradient magnitude is very small, we know that the slope is nearly flat and that we’re close to a local minimum so we stop iterating at this point.
A great intuition for this is imaging that you're walking down a hill. As you approach the bottom, the ground becomes less steep. When the slope is almost flat, you know that further movement in any direction won't significantly lower your position and so you stop.
This ends Part 2 of this series. In Part 3, we will continue our dive into more optimization algorithms. Below is a section summary discussing the key points which we went over for anyone needing a review.
Section Summary
Descent direction methods incrementally descend toward a local optimum: the don’t guarantee finding the global minimum or maximum, but they are effective in finding a local optimum by progressively moving in the direction that most reduces a function’s value.
Approximate line search can be used to identify appropriate descent step sizes: Exact line search methods can be time-consuming because they require finding the precise best step size. Approximate line search offers a quicker alternative by finding a "good enough" step size that reduces the function value sufficiently without needing to be perfect. Approximate line search strikes a balance between accuracy and efficiency, making it a practical choice for selecting step sizes in optimization algorithms.
Trust region methods constrain the step to lie within a local region that expands or contracts based on predictive accuracy: Trust region methods involve limiting your steps to a local area (the "trust region") where the function is well-behaved and easier to model. The size of this region adjusts dynamically based on how accurately your model predicts changes in the function's value. They help maintain control over the optimization process by adapting the step size based on how well your predictions match reality, reducing the risk of making large, inaccurate steps.
Termination conditions for descent methods can be based on criteria such as the change in the objective function value or the magnitude of the gradient: Termination conditions determine when to stop the optimization process, and 4 key ones used in descent methods are provided below:
Maximum Number of Iterations: Stop after a fixed number of steps to prevent the algorithm from running indefinitely.
Small Change in Objective Function Value: Stop when further changes to the function value are insignificant.
Small Step Size: Stop when the algorithm is taking tiny steps, suggesting convergence.
Small Gradient Magnitude: Stop when the slope is nearly flat, indicating you're close to a local optimum.
I’m currently working on a a visual-focused cheat sheet dealing with algorithms which I’ll try to make available soon. This will be a continuation of my Visual Data Structures Cheat Sheet. If you enjoyed reading this, please like an subscribe and thank you!